量子自旋液体是诺贝尔获得者P. W. Anderson在1973年首次提出的一种即使在零温下也不会发生对称性自发破缺的量子态。高温超导发现之后，Anderson又尝试从量子自旋液体角度来理解高温超导的机理，由此进一步引发了对量子自旋液体的研究兴趣。近年来，随着大量强阻挫量子自旋材料的发现，对量子自旋液体态的研究正成为凝聚态物理研究的一个热点方向。这方面的研究之所以重要，有两个原因。其一，这种量子态不能用传统的朗道对称破缺理论来描述，对它的研究有可能改写朗道的相变理论；其二，自旋液体具有拓扑量子序，元激发是分数化的，是实现拓扑量子计算的可能载体，有重要的应用前景。
　　Kagome晶格上的反铁磁系统具有强烈的几何阻挫和量子涨落，是发现量子自旋液体的理想材料。在过去的20多年里，从理论分析到数值计算，以及实验测量等各个方面对它进行了大量的研究。在一些具有Kagome晶格结构的材料中，也发现了一些量子自旋液体的特征。但对这个系统中的量子自旋液体态的本质，仍然存在许多争议，特别是关于低能激发是否存在能隙的问题一直没有达成共识。由于这个系统的几何阻挫和量子涨落特别强，量子场论的方法难以提供定量分析的结果；在数值计算方面，量子蒙特卡罗方法存在负符号问题，密度矩阵重正化群方法虽然在研究一维问题上很成功，但在二维受有限尺寸效应的限制，也难以给出无可争议的计算结果。
　　为了解决Kagome格子上的量子自旋液体及其它二维强关联问题，中国科学院物理研究所/北京凝聚态物理国家实验室（筹）凝聚态理论与计算重点实验室的向涛研究员及其研究组近年来一直在致力于发展一种被称之为“张量重正化群”的多体量子计算方法。这种方法没有负符号问题，而且可以直接模拟无限大系统，也没有有限尺寸效应导致的不确定性。最近，他与廖海军博士后，中国人民大学谢志远副教授和瑞士保罗-谢尔研究所Bruce Normand教授等组成的研究团队，在他们2014年提出的一种新的张量网络态的波函数表示基础上【Phys. Rev. X4, 011025 (2014)】，运用张量重正化群方法对 Kagome格子上的海森堡模型进行了大规模的数值计算研究。
　　在张量重正化群中，有一个很重要的参数，就是每个格点上张量的维数D。这个参数决定了张量网络态的精度。D越大，精度越高。但D越大，计算的复杂度也越高。在过去的计算中，最大能够处理的张量维数一般不超过13（D=13这个值也是在不考虑对称性的前提下，向涛研究组长期保持的一个纪录），很难对Kagome反铁磁的激发是否存在能隙给出准确的判断。为了解决这个问题，他们提出了一种新的张量重正化群计算方法，第一次把D从13提高到25（如图1所示）。这一关键性的突破对确定能量和磁化强度随D的变化行为起了至关重要作用。基于这个高精度的计算结果，他们发现Kagome反铁磁体的基态是一个无能隙的量子自旋液体，而不是有能隙的量子自旋液体，解决了这个长期争论的问题。
　　这项研究成果最近发表在Physical Review Letters 118, 137202 (2017)，并被选为编辑推荐文章，同时美国物理学会“Physics”网站上发表了美国伊利罗伊大学Bryan Clark教授写的一篇题为“Closing in on the Kagome magnet”的观点（Viewpoint）”文章，对这项工作做了详细的介绍[29 March 2017 Physics 10, 33 http://physics.aps.org/articles/v10/33]。 这个题目有双重寓意（见图3），一是表示Kagome反铁磁的能隙被关闭了，二是表示Kagome反铁磁这个问题接近最终解决了。
　　上述工作得到了国家自然科学基金委（10934008, 10874215, 11174365）、科技部的项目（2012CB921704, 2011CB309703, 2016YFA0300503）和中国科学院的支持。

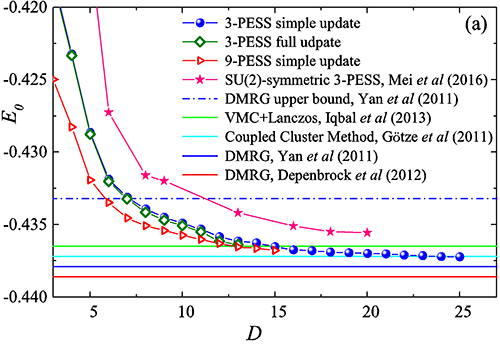图1. Kagome反铁磁海森堡模型的基态能量随张量维数D的变化行为。图中分别显示了D保留到25的3-PESS simple update结果，D保留到13的3-PESS full update结果，D保留到15的9-PESS simple update结果，同时也显示了与其他数值结果的比较。

图2. 包含次近邻相互作用Kagome反铁磁海森堡模型的磁化强度M随J2的变化行为（D=9,12,15），及其与D=∞的Husimi晶格结果的比较。

图3. 美国伊利罗伊大学Bryan Clark在Physics 10, 33 (2017)发表的“观点”文章中的一张示意图。说明随着张量维数D的增加，波函数的能量越来越精确，因此对Kagome反铁磁问题的理解也变得越来越清晰。图中绿色的图案就是Kagome格子。