核心提示:有了量子场论,人们才能从某种程度上说真正理解了电荷的本质。
我们或许在很小的时候就知道,这个世界有正负两种电荷,带同种电荷的物体相斥,带异种电荷的物体相吸。我们还知道,电子带负电荷,质子带正电荷。但事实上,对于电荷的本质,可能大多数人并不清楚。虽然电荷的概念已经有了数百年,但是直到上个世纪中期,有了量子场论,人们才能从某种程度上说真正理解了电荷的本质。而今天的主题就是揭开这个我们既熟悉又陌生的电荷的真正面纱。

一、写在前面
在正式讨论电荷的本质之前,我们有必要先阐述关于现代物理学研究的一个基本思想:现代物理学在评判一个理论的正确性或成功性时,最重要的标准是该理论本身的自洽性和能否很好地解释实验规律,因此,即使该理论违背了直觉或一些早已在人们心中根深蒂固的“事实”,那也在很大一部分程度上也是可以接受的。
就拿电子和声子的例子来说吧。现在人们基本承认电子是一种基本粒子,但事实上我们并没有亲眼看到电子长得什么样,是圆的?还是方的?我们唯一清楚的是根据探测器探测到的数据可以肯定某粒子的行为跟我们定义出来的电子的行为是一模一样的;而对于声子,我们则普遍认为它是一种准粒子,并非真实存在的,但另一方面,从探测器上的数据来看它确实完全可以认为是一种真实存在的粒子。因此,从某种程度上来说,“电子不一定真,声子不一定假”。这看起来似乎很荒诞,但并不碍事,其实无论是真实粒子还是准粒子,只不过是定义上的差别,其理论本身则是自洽的并能很好地解释各种实验现象,那我们就不能因为这个定义看起来很不符合直觉就认为它是错的。我们的物理实质是不应该依赖于选择什么表象的(物理实质只能是实验现象和数据),而对于各种物理量的定义从某种意义上来说就是一种表象。既然不依赖于表象,我们当然是选择一种最简单直观的表象来理解我们的世界咯,比如说定义粒子的电荷就能很好得解释各种电磁现象了,何乐而不为?
所以,真正的好的理论或伟大的理论,并不是它能够推翻人们先前对这个世界的某些认识,或其多么晦涩难懂,而是,首先它是自洽的并且能够完美地解释和预测实验,其次它是简洁直观的。这里的直观不是说它一定要符合直觉,而是物理过程是可以直接从该理论中读出来,比如在狄拉克方程中,反粒子的概念可以直接从方程式中得出来,这就是所谓的直观。
二、诺特定理

艾米·诺特(Emmy Noether,1882-1935,德国数学家),作为20世纪最伟大的女性数学家,被誉为“抽象代数之母”,其在物理学领域也有一项具有划时代意义的工作,即我们将要阐述的诺特定理。
诺特定理是将物理中的守恒量与对称性联系起来的一个理论,即,系统的任何一个连续对称性都能对应一种守恒量(这里必须是连续对称性)。比如说,对于自由粒子体系,它有空间平移对称性,因此它就对应了系统动量守恒;对于保守力场体系,它有时间平移对称性,因此它就对应了系统能量守恒;对于有心力场体系,它有空间旋转对称性,因此它就对应了系统角动量守恒。
事实上,这些守恒量我们统称为守恒荷,将这些荷的空间分布密度定义为荷密度ρ,对荷密度进行全空间积分便得到系统总的荷量。而一般情况下空间中的荷是一直在空间流动的,这样这些荷就形成了流(具体物理图像,读者可参考水流和电流的物理过程,可以从中类比过来)。那么,若系统具有某种对称性,根据诺特定理,我们可以推导出如下的守恒荷方程:
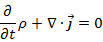
或积分形式:

第一个方程的物理意义是空间所有点的荷密度变化率等于该点流入或流出的荷密度的速率,也就是说该体系是一个保守体系,没有任何荷从该系统中消失也没有额外的荷进入到该体系,因此该系统的总的荷是守恒的(其实,第二个积分方程更能十分直观反映荷守恒的结论,但不如微分方程给出的物理过程那么清晰)。其实,这也就是电荷守恒的微分和积分形式。
注:对称性是现代物理学理论中的一个极其重要的概念,其表示在经过某些变换时,系统状态保持不变,而这里系统的状态则是由系统的欧拉-拉格朗日方程(又称运动方程)所描写的。例如,对于保守场体系,系统的拉格朗日量不显含时,从而它的运动方程也只含有时间的偏导项,因此对时间进行平移变换(即t→t+T的变换,这样,对时间的偏导项会保持不变),运动方程自然保持原来的形式,所以我们说该保守系统具有时间平移对称性。
三、电荷的本质
读到这,相信很多读者可能已经对电荷有了一些似是而非的理解了。是的,同能量、动量和角动量一样,电荷也是来自于一种连续的对称性,叫做全局的U(1)规范对称性。该对称性与能量、动量及角动量所对应的时间平移、空间平移和空间旋转对称性是有很大区别的,后者的对称性都是和时空相关的,都被称为时空对称性,而前者的对称性则与时空无关,被称为内禀对称性。因此,我们也称粒子的电荷是一种内禀的属性与时空无关。
那么,何为全局的U(1)规范对称性?我们知道,在量子场论中,粒子的行为是由该粒子的场算符所描写的,而对于很多粒子来说,它的场算符是由一对互为厄米共轭的复的场算符和来表示,比如电子。全局的U(1)规范变换,即是对场算符做的变化,即在场算符前加一个全局的相位因子(这里的α是一个任意的与坐标无关的实参数,若其与空间坐标有关则被称为局域的U(1)规范变换,这里不予讨论)。若在这种变化下,即α 取任何实数,系统的运动方程都保持不变,那么称该体系具有全局的U(1)规范对称性。
这样,我们可以根据相关的数学计算,将全局的U(1)规范对称性所对应的守恒荷的相关算符形式给求出来。例如,对于自由的电子场,根据诺特定理,通过计算我们可以得到如下的守恒荷的算符形式:

其中, \(a_{p}^{s\dagger },a_{p}^{s},b_{p}^{s\dagger },b_{p}^{s}\)分别是电子与正电子(电子的反粒子)的产生、湮灭算符,s表示电子的自旋。显然将Q算符作用在电子的单粒子态上,我们得到单电子的该荷量是+1,作用在正电子的单粒子态上,得到正电子的单粒子荷量为-1,也就是说电子与正电子所带的这种荷大小相等,符号相反,而这一结论可以推广的所有粒子中。这里,大家可能发现了,我们仅仅给出了该荷的形式上的量子化关系,并不能计算出电子实际所带的该荷量的大小和其物理意义。这是由于我们上面所讨论的是自由电子场,并没有引入相互作用。当我们将电子场与电磁场进行耦合,即引入电磁相互作用时,我们发现电子所带的该种荷与我们先前定义的电荷的行为是完全一样的,因此,我们认为电子的该守恒荷就是我们所说得电荷。实际上,从电磁相互作用的拉格朗日量中我们可以看出,单粒子的电荷量大小影响着该粒子与电磁场的耦合强度(及QED的耦合系数),二者是成正比的。推广到经典极限下,粒子的电荷就表征着库伦力的大小和方向。总之,我们认为,电荷的本质是来源于粒子的全局U(1)规范对称性(其实反过来并不一定成立,也就是说并不是所有粒子的全局的U(1)规范对称性的守恒荷都是电荷,只有在是与电磁场耦合的意义下的全局的U(1)规范对称性的守恒荷才是电荷),是个内禀属性,其大小仅依赖于粒子种类,而不依赖于该粒子的时空坐标系选择,即对于一个确定的粒子来说,其电荷量是常量,且互为正反粒子所带的电荷量大小相等符号相反。
至此,或许有些读者表示很不满,认为这种意义下的电荷的本质不过只是一些数学上的小把戏。我们依旧看不清,摸不着,我们甚至怀疑其是否真正存在。然而,正如笔者前面所说的,同声子的概念一样,当我们有了电荷的概念以后,似乎一切物理图像都变得清晰了,并且整个体系是显得如此自洽、直观和完美,在这种意义下,我们为何不认为电荷就是真实存在的呢?或者说,如果不能获得其他什么价值,我们又有什么必要去认为电荷不是真实存在的呢?最后,笔者想引用一下狄拉克先生的一句名言:“这么漂亮的东西不可能是错的。”
