量子自旋液体是存在于量子阻挫磁体中的一种新型物质形态，它的一个突出特点就是其中蕴含着各种分数化的元激发。然而，作为拓扑序的材料实现，量子自旋液体一直以来就因其不存在局域的可观测量而成为实验探测上的“痛点”。最近，由中国科学院物理研究所/北京凝聚态物理国家研究中心凝聚态理论与材料计算重点实验室博士生孙光宇、博士后王艳成（已出站，现为中国矿业大学讲师）、孟子杨副研究员、方辰副研究员和复旦大学戚扬副教授与耶鲁大学的程蒙助理教授等人组成的研究团队（以下简称该团队），运用大规模的量子蒙特卡洛计算和规范场理论分析，在二维量子自旋液体动力学的理论研究上取得了具有实验指导意义的进展。
　　他们结合数值模拟和理论分析研究了具有Z2 拓扑序的量子自旋液体，确认了其中的 spinon 和 vison任意子激发以及vison在不同的晶格平移对称性分数化之下的动力学行为。他们采用了kagome晶格上强阻挫的量子自旋模型，此模型可以通过调节磁场很方便的得到具有不同静磁矩(m=0和m=1/6)的Z2量子自旋液体。而在静磁矩m=0与m=1/6情况下，又可以分别导出对应vison平移算符的反对易与对易关系。在m=0时，由vison凝聚所驱动的从自旋液体相向共振价键（VBS）相的转变过程中，平移算符反对易关系意味着此时 vison 波函数具有平移对称性的分数化，而分数化反映在动力学性质中就是系统自旋激发谱上动量为 Γ点和动量为M点的能隙同时关闭；同时，反映在系统的静态自旋结构因子上，不仅在Γ点有峰，而且在M点也会出现一个峰。与之对应的是，在静磁矩m=1/6时，因为 vison 波函数平移对称性没有分数化，系统的自旋激发谱只会在 Γ 点上的关闭能隙，而在M点并无信号出现，在其静态自旋结构因子上亦如是。
　　该团队运用大规模的量子蒙特卡洛模拟并结合随机解析延拓的方法，首次将S+S-和SzSz这两个组分的动力学自旋激发谱分别与成对的自旋子（spinon）和vison元激发谱对应起来。进而，通过对vison元激发谱在量子自旋液体到VBS态相变点附近的性质研究，他们证实了在m=0 的量子自旋液体中，系统的平移对称性发生了分数化；而在 m=1/6 的量子自旋液体中，平移对称性没有发生分数化。这就证明任意子所携带的对称性分数化信息可以在自旋激发谱中找到答案。鉴于这些动力学计算结果可以与实验上采用中子散射以及共振x射线衍射等手段得到动力学特征进行对比，该团队这项数值计算和理论分析工作，不仅在量子自旋液体的理论研究上有所进步，并且对目前正在快速发展之中的阻挫磁体和量子自旋液体等领域的相关实验工作也具有指导意义。
　　相关工作发表在最近一期的《物理评论快报》上（Phys. Rev. Lett. (2018))。这项工作得到了科技部重点研发计划2016YFA0300502，2015CB921700，自然科学基金委项目11421092、11574359、11674370, 中科院先导培育项目 XDPB083 的支持。量子蒙特卡洛模拟所需的大规模的并行计算在中科院物理所量子模拟科学中心和天津国家超算中心天河1号平台上完成，计算过程中得到了天津国家超算中心孟祥飞博士、赵洋工程师等人的有力配合，在此一并感谢。

Fig.1 (a) Kagome 晶格量子自旋液体模型。 (b) Kagome 晶格的布里渊区，Γ, M, K 为布里渊区中的高对称点。(c) 和 (d) 是模型的基态相图。其中 (c) 为外磁场为零的情况，系统没有静磁矩 m=0。(d) 为外磁场不为零的情况，系统的静磁矩 m=1/6。沿着图中的红线，两种量子自旋液体都会发生 vison 凝聚的相变进入对称性破缺的共振价键 (VBS) 相。

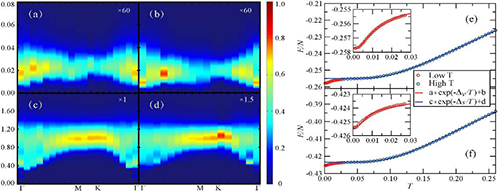Fig.2(a),(b)是量子自旋液体中沿着高对称线的SzSz的激发连续谱（对应成对vison激发谱），(c),(d)则是S+S-的谱（对应成对自旋子（spinon）激发谱）。(a),(c)外磁场为零m=0，(b),(d)外磁场不为零m=1/6。(e), (f)为其中的能量温度依赖关系。通过拟合能量温度依赖关系所得到的这两种任意子的能隙与谱中的能隙大小是一致的

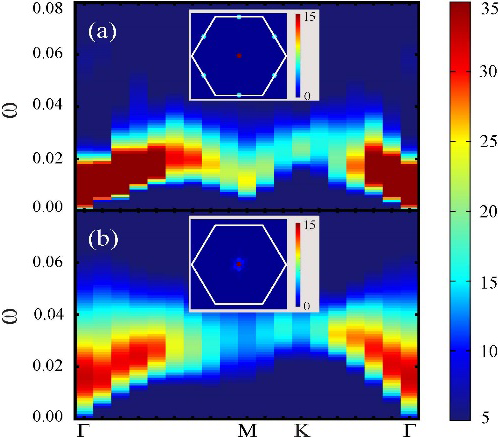Fig.3(a),(b)是量子自旋液体中QSL-VBS 相变点附近的自旋激发谱对应成对vison激发谱。(a)外磁场为零m=0，(b)外磁场不为零m=1/6。m=0的自旋激发谱在动量空间中Γ, M点都有能隙关闭的迹象，而1/6则只在Γ点关闭，即平移对称性分数化模式的不同。小图中的静态自旋结构因子也反映了这点。