本文经「原理」(微信公众号:principia1687)授权转载,
禁止二次转载。
在不同尺度上,物理世界遵循着不同的规律。描述微观量子世界的定律,与描述宏观物体的定律有着本质的区别。然而,任何随着尺度的变化必然是连续的,物理学中看似截然分立的领域,实则具有丰富的联系。
《尺度,法则和生命》这幅画,正是通过17个地位显著的公式,描绘了物理学不同领域的联系与相互影响。

○ 《尺度、法则和生命》。由于原图中有部分错误,现在看到的是小编修正以后的版本。| 图片来源:Sean Lang
沿着图中从左到右的方向,粒子数量增加,系统复杂性也随之增加。沿着从下往上的方向,系统的尺度逐渐增大。图的各个角分表代表了物理学的不同领域。沿着顺时针方向,左下角描绘粒子波动性的图像代表量子力学; 左上角电磁相互感生的图像代表电磁学与电动力学;旁边的湍流代表流体力学;右上角的星云、黑洞、恒星以及交织的时空,代表描述宇宙的相对论;右下角纷乱的粒子、石墨烯、足球烯、DNA双螺旋代表热力学与统计物理。
图的正中是人类和孕育人类生命的地球。地球上的四个人则表现了人类面对这四个不同尺度与复杂性的领域时,截然不同的态度:左上角的人拿着笔,陶醉于电动力学的完美,右上角的人满含热情与虔诚地拥抱宇宙的奥秘,右下角的人面对复杂的世界充满困惑,左下角的人震惊于微观量子世界的怪异。
画面四个象限间隔用黑白色调,具有旋转对称性,仿佛阴阳一样形成一种动态的平衡。
本文将从左上角开始,顺时针依次介绍这些描述了不同尺度自然世界的重要公式。
1. 麦克斯韦方程组
\(\nabla \cdot E=\frac{\rho}{\varepsilon_{0}}\)
\(\nabla \cdot B=0\)
\(\nabla \times E=-\frac{\partial B}{\partial t}\)
\(\nabla \times B=\mu_{0} J+\mu_{0} \varepsilon_{0} \frac{\partial E}{\partial t}\)
○ 麦克斯韦方程组,位于画作中的左上角。更多相关介绍请见《那个名为“又大又好”的方程组,真的是又大又好!》
电磁现象研究中最重要的一点是要理解,是电荷的存在产生了渗透整个空间的电磁场。
在上图显示的四个方程中,有两个方程中有倒三角、点,以及表示电场和磁场的字母E和B。这两个公式描述了电场和磁场的散度,或者说是点源在径向上产生磁场和电场的能力。根据这两个公式,电场的散度取决于存在的电荷数量,而磁场的散度总是零!这意味着电场是有源的,而磁场是无源的,正如我们知道的,自然中存在点电荷,但是不存在磁单极子。
另外两个等式包含叉号而非圆点,描述电场和磁场的旋度。旋度可以理解为电场与磁场在自由空间弯曲程度的度量。在描述电场旋度的等式右侧包含磁场,在描述磁场旋度的等式右侧包含电场。这表明,随时间变化的电场会激发环绕的磁场,而随时间变化的磁场会激发环绕的电场。
在描述磁场旋度的等式中,还有一个额外的 ∂E/∂t 项,代表位移电流,这表示运动的电荷会产生环绕的磁场。值得注意的是,在描述电场旋度的等式中,并不包含对应的“磁流”项,这是因为“磁流”根本就不存在!如果存在磁单极子,就会有“磁流”,而磁单极子迄今仍未被发现。
这四个描述电磁场散度和旋度的等式构成了麦克斯韦方程组,它们为电磁场在电荷存在时或者真空中的行为提供了完整的描述。
2. 纳维尔-斯托克斯方程
\(\partial_{t} V+(V \cdot \nabla) V-\nu \nabla^{2} V=-\frac{1}{\rho} \nabla P+f\)
○ 纳维尔-斯托克斯方程,位于画作上方中间位置。左侧包含与流体速度、加速度有关的项,而右侧是与外力、外部压强有关的项,形式上与牛顿第二定律非常一致。
上面这个看起来十分冗长的等式便是描述流体运动的纳维尔-斯托克斯方程。流体,简单说来,就是运动的连续粒子流。正如牛顿第二定律 (F=ma) 描述了粒子在力的作用下如何运动一样,纳维尔-斯托克斯方程描述了粘性、不可压缩流体的运动。它并不是在表述能量守恒,而是描述流体在给定的粘度、集体速度和外部压强下是如何运动的。
由于非线性偏微分方程的数学形式,纳维尔-斯托克斯方程令无数相关领域的研究人员头疼不已。纳维尔-斯托克斯方程的存在性与平滑性是千禧年七大数学难题之一,普遍认为,距离方程的解决还很遥远。
3. 连续性方程
\(\frac{\partial \rho}{\partial t}+\nabla \cdot j=\sigma\)
○ 连续性方程位于纳维尔-斯托克斯方程下方,在顶部的两个人体中间。
流体力学中,决定流体行为的一个重要特征,是在流体中是否存在源(source)或者汇(sink)。想象流体中的一个封闭空间,我们可以问如下的问题:在一段时间内,有多少流体进入这个空间,有多少流出?
如果是一根没有洞的水管,可以确定流入和流出的流体量是相等的,因为流体是连续的!在这种情况下,连续性方程中代表流体源或汇的希腊字母σ等于零。从左往右,方程中另外两项分别代表单位时间内流入或流出封闭空间的流体量,以及流体的散度。连续性方程实质上是流体总量守恒的一种表述,描述了流体不会凭空产生或者消失。
4. 洛伦兹变换
\(X^{\prime}=\Lambda X\)
○ 洛伦兹变换的公式位于纳维尔-斯托克斯方程上方,在中间的格点图形那里。
在爱因斯坦提出狭义相对论之前,理解物体相对运动是通过伽利略变换。在伽利略变换的图景中,对运动物体时间和空间的描述不包括时间膨胀和长度收缩效应。
爱因斯坦假定在所有惯性系中光速是恒定的, 并且构架了一种和伽利略变换不同性质的变换,后来被称为洛伦兹变换。这种变换解释了如下事实:在静止参考系中,运动物体在时空中的前进速度是不同的,这与运动参考系和静止参考系的相对速度有关。
如图中的洛伦兹变换公式中表示的那样,大写的X和X’代表观察者和被观察的时空坐标。大写的希腊字母Λ是4×4的变换矩阵,它包含了物体与观察者相对速度的信息。
5. 爱因斯坦广义场方程
\(R_{\mu \nu}-\frac{1}{2} R g_{\mu \nu}+\Lambda g_{\mu \nu}=\frac{8 \pi G}{c^{4}} T_{\mu \nu}\)
○ 爱因斯坦广义场方程位于画作右上角,黑洞下方。
在广义相对论中,爱因斯坦场方程描述了在物质和能量的影响下,时空结构是如何弯曲缠绕的。可以从方程中求解出的小写字母g代表时空度量(space-time metric),时空度量g可以认为是特定系统中时空结构的特征描述。爱因斯坦说“一只盲目的甲虫,在球面上爬行,它意识不到它走过的路是弯曲的。”时空度量g就是这个球面弯曲形状的表征。如果是一只非常非常聪明的甲虫,它知道这个面的g和相关知识,也就知道了自己在什么形状的面上爬行。
通过时空度量,我们可以确定物体在系统中的行为,因为,最简单说来,时空曲率会引导物体的运动。这种“引导”由物体周围时空结构的曲率决定,正是我们感受到的重力。
6. 黑洞的贝肯斯坦-霍金熵
\(S=\frac{c^{3} A}{4 G \hbar}\)
○ 贝肯斯坦-霍金熵的公式位于图的右上角,黑洞上方的位置。
当霍金还年轻的时候,他设想了一种机制,通过这种机制,黑洞喷射自身的质量,并最终蒸发消失。这种想法基于透过量子力学“透镜”观察到的真空特性。
根据我们对量子力学的理解,真空中充满了正负粒子对,它们不断地成对产生或湮灭。霍金的理论表明,如果这种现象出现在史瓦西半径附近 (光和粒子均无法逃离时的黑洞半径称为史瓦西半径),正负粒子对中的一个会掉入黑洞,另一个则会逃离。根据这一机制,黑洞就像是在喷射自身的质量,这种现象被称为霍金辐射。
贝肯斯坦-霍金熵描述了在黑洞表面所必须的熵,以符合控制黑洞视界物质外部的热力学原理。
7. 爱因斯坦质能方程
\(E=m c^{2}\)
○ 爱因斯坦质能方程位于右上角的行星里,就在爱因斯坦场方程下方。
爱因斯坦质能方程可能是物理学中最广为人知的方程。尽管名字广为流传,它的物理内涵却有些令人难以捉摸,只有通过相对论才能理解。这个等式之所以如此重要,是因为它直观的表述了对于静止物体,能量就是质量,质量就是能量。与物体本身相对静止的参考系内的质量,称为物体的静止质量。
一个更普适的质能关系是:
\(E_{r}=\sqrt{\left(m_{0} c^{2}\right)^{2}+(p c)^{2}}\)
其中m₀是静止质量,p是动量。对于质量为零的物体,比如光子,m₀等于零,公式简化为E=pc。当物体的运动速度远小于光速时,动量p很小,公式回归到图中的形式, E=mc²,这正是宏观世界物体近似遵循的规律。
8. 重整化群方程
\(\frac{d g}{d \ln (\mu)}=\beta(g)\)
○ 这个方程被放在了图的中间,分裂在地球的两侧。
重整化群方程可以用来确定物理系统在不同尺度上的行为。类似于显微镜是观察细菌的合适工具,却不适合观察宏观物体,这个方程是用来确定,在特定的物理尺度或能量尺度上,应用什么数学工具更为合适。
这个方程可以用于研究,当系统的尺度发生变化时,一个理论的相关参数应如何变化。另外,这个方程可以表明,哪些理论在所有能量尺度上是有效的——例如共形场论(conformal field theory)——这些理论在物理学的众多领域具有重要作用,包括凝聚态物理、弦论、规范-引力对偶(全息原理)。
9. 牛顿第二定律
\(F=m a \quad F=\frac{d p}{d t}\)
○ 牛顿第二定律在图中航天飞机的右边。
在宏观尺度下,当物体运动的速度远小于光速,作用于物体上的力等于物体的质量乘以加速度。牛顿第二定律是人们理解力这一概念的基础,被应用在难以计数的研究领域中。
在牛顿第二定律F=ma下方,是作用于物体上的力的更为普适的表达。这个公式表达的是,作用于物体上的力等于单位时间内物体动量的变化。这种表达之所以更为普适,是因为它不仅包含了特定质量物体速度变化的可能,还包含了物体质量变化的可能。因为动量由质量和速度共同决定,这两者中任何一种的变化,都意味着有力作用于物体上。
在画作中,画家让F=ma和F=dp/dt这两种表达互相排斥,来描述牛顿第三定律的内涵。在没有外界影响的情况下,对于任何一个力,都存在一个大小相等、方向相反的力。
10. 热力学第二定律
\(\Delta S>0\)
○ 热力学第二定律位于DNA双螺旋下面。
热力学第二定律陈述的是,热力学系统从一个平衡态到另一平衡态的过程中,其熵永不减少:若过程可逆,则熵不变;若不可逆,则熵增加。简单的说,熵是衡量系统可以采取的排列方式的量。想象密封盒子里的一团粒子,与外界不存在能量交换。与所有粒子都聚集在盒子的一个角落相比,粒子分散在整个盒子中时,可能的排列数量远远大得多。这也和我们的直观经验相吻合,比如一团气体会自动扩散开来。虽然这不是在孤立系统中,推动这一过程的仍是熵的增加。这就是热力学第二定律最核心的思想。孤立系统有一种倾向,就是演化成具有最多可能排列数量的状态。
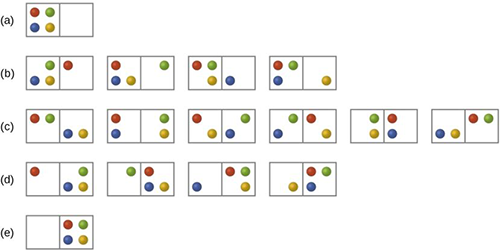
○ (c)的可能排列最多,熵最大。 | 图片来源:https://chem.libretexts.org/
11. 配分函数
\(Z=\sum_{i} e^{-\beta E_{i}}\)
○ 配分函数在图的右下角。
当确定系统处于某个特定状态,尤其是平衡态的概率时,配分函数是我们最好用的工具。配分函数取决于系统的自由度,以及表征系统的状态是连续或者分立。从统计力学的角度,最重要的描述系统的物理量,如自由能、熵、压强等,都能通过配分函数及其导数来表达。配分函数被认为包含系统的所有信息,所以一旦知道配分函数,系统的任何性质原则上都能够计算出来。但是复杂系统的配分函数并不容易获得。
12. 量子简谐振子
\(\hat{H}=\hbar \omega\left(\hat{N}+\frac{1}{2}\right)\)
○ 量子简谐振子的表达式在地球下方,图的中间。
最简单的简谐振子是单摆,摆臂在重力作用下持续均匀摆动。量子简谐振子和宏观摆的本质区别在于,对于量子简谐振子,振动的物体是像电子这样的粒子,且粒子的振动限定在一系列离散的状态上。不同于宏观的摆可以具有任何频率,量子简谐振子中的粒子只能具有特定的离散的频率。这个概念描述了量子力学与量子尺度的物质粒子的根本特性。画家用抛物线来代表简谐振子,因为对于简谐振子的定义就是势阱禁锢着振动的粒子。
如图中所表达的,量子简谐振子中占据特定能量状态的电子跃迁到较低能量态时,一个光子会发射出来,其能量恰好等于两个状态的能量差。光子的波长与其能量相对应,较高能量的光子具有较短的波长。这个过程也可以反向进行。一个光子可以与电子相互作用,将电子激发到较高能量态,电子能量的增加则等于光子携带的能量。
13. 最小作用量原理
\(\delta \int_{t_{1}}^{t_{2}} L(q, \dot{q}, t) d t=0\)
○ 最小作用量原理在图的中下方。
最小作用量原理代表了我们对于物理学几乎所有领域的最深刻理解。最小作用量原理本质上表达的是,我们可以通过提出一个问题来确定物理系统的行为,这个问题就是,自然是否在追求某个量的最小化?或者更普遍的,自然是否在寻求某种不变性?
关于最小作用量原理的一个绝佳例子是光的折射现象。当光线从一种介质进入另一种介质(比如从水进入空气)中时,会选取怎样的路径呢?事实是,光线会选取传播时间最少的路径!因为光在不同介质中传播速度不同,为了使传播时间最短,光线会在界面上发生弯折,以确保在光速快的介质中通过更多路程。理解了最小作用量原理,也就理解了光的折射现象。
这绝非最小化原理在物理学中的唯一例证。事实上,最小化原理广泛地应用于经典力学、电磁学、广义相对论、量子力学和很多其他领域。在所有尺度上,自然似乎都在告诉我们,确定一个复杂系统行为的最简单方法是类似这样的最小化原理。
14. 薛定谔方程
\(\hat{H} \psi=E \psi\)
○ 薛定谔方程位于图中左下角的波形中。
薛定谔方程是量子力学的精华,以简洁的数学形式表达了量子力学的内涵,描述在自由空间或者存在势能的情况下粒子类似于波的行为。画家以最简洁的形式表达薛定谔方程:哈密顿算子H作用于波函数Ψ,等于系统的总能量E乘以波函数Ψ。波函数包含关于量子系统能量状态的概率信息,当不同的算符作用于波函数时,可以得到系统的能量、角动量等物理量。
15. 海森堡不确定性原理
\(\sigma_{x} \sigma_{p} \geq \frac{\hbar}{2}\)
○ 海森堡不确定性原理位于图的左下角。
海森堡不确定性原理陈述的是:由于在量子尺度上粒子具有波的特性,粒子的动量和位置不能同时精确测定。
首先,在你的脑海中想象一列波在空间传播,比如石子投入水中引起的涟漪,或者振动的琴弦。问自己如下的问题:波的准确位置在哪里?你想象的波具有固定的波长,不是吗?具有固定波长的波具有精确的动量,然而却不具有精确的位置,无法准确说出这列波究竟在这里,还是在那里。
现在,想象一个波包,也就是许多各种波长的波叠加在一起形成的具有确定位置的波。这时,波包有着更为精确的位置。但是,因为添加了许多不同波长的波,波包动量的不确定性增加了。这就是不确定性原理的本质。
画家在这幅图中用标准差σ来表示位置和动量的不确定性,位置和动量标准差的乘积大于或等于一个常数(普朗克常数的一半)。因此,当一个量变得精确时(σ变小),另一个量的精确性会相应降低(σ变大)。
16. 狄拉克方程
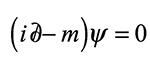
○ 狄拉克方程在画作的左侧,爆炸的下方。
1928年,保罗•狄拉克提出了描述电子的相对论性方程式——狄拉克方程。它把物理学上两个最重要的想法联姻在了一起:描述微观世界的量子力学以及描述快速运动物体行为的狭义相对论。因此,狄拉克方程描述了粒子(比如电子)以接近光速运动时的行为。狄拉克方程是通往量子场论的第一步,以至于有了今天的粒子物理学的标准模型。此外,狄拉克方程还包含了解释粒子自旋特性的必要细节,并且预言了反物质的存在!
17. 光电效应
\(E=h f-\phi\)
○ 光电效应的公式在图的左侧,爆炸的上方。
相比于相对论,爱因斯坦对光电效应的发现并不那么广为人知,然而正是凭借光电效应的工作,爱因斯坦获得了他唯一的诺贝尔奖。
光电效应描述的是,当光子照射到金属表面上时,电子携带着动能,从金属表面发射出来。然而,光电效应令人惊异的洞察是,发射电子所携带的动能并不取决于光的强度,而是取决于光的频率。这是引领物理学家提出离散能量状态这一概念的重要线索,正如后来量子力学中描述的那样。
在这幅画中,光子的能量表示为普朗克常数和频率的乘积。出射电子的动能E等于光子的能量减去功函数φ。功函数φ是电子从金属表面的束缚能量状态挣脱所需要的能量,它是一个常数,与入射光子的能量无关。 也就是说,入射光子的一部分能量用于克服金属对电子的吸引,剩余的能量则转化为出射电子的动能。
参考来源:https://publish.illinois.edu/flowing-from-quantum-to-cosmic/the-equations/
来源:原理
