因对称性破缺而出现的有序电子态是凝聚态物理研究中俯拾皆是的基本现象。类比于液晶中的向列相，物理学家提出在关联电子材料中同样可能存在类似的“电子向列相”，即由于电子相互作用，系统呈现出打破晶格固有的旋转对称性的电子态。在铁基超导材料中，随温度的降低，其母体大多将经历从四重对称的四方相到二重对称的正交相的结构相变，并随后发生从顺磁态到共线型反铁磁态的磁性相变。通过引入掺杂或压力，结构相变和反铁磁相变会逐渐被压制，超导随之出现，并且在结构和磁相变消失的临界点附近达到最高的超导转变温度。目前，许多实验研究揭示了铁基超导体中电子态性质(如电阻、红外光谱、轨道能级、杨氏模量等)有着显著的铁砷/铁硒面内二重对称特征，甚至持续到四重对称的高温四方相中，表明结构相变是由电子自由度而非晶格自由度驱动的，来源于旋转对称破缺的电子向列相。然而，向列型电子态相变的驱动力是轨道还是自旋自由度，仍有很大争议，向列型电子态涨落与超导电性是否存在直接关联也尚不清楚。认识清楚电子向列相的物理起源，对理解铁基材料中的结构相变机理、磁性物理及高温超导电性均至关重要。
　　最近，中国科学院物理研究所／北京凝聚态物理国家实验室(筹)SC8研究组在BaFe_2-xNi_xAs₂体系中电子向列相研究方面取得两项进展。在向列相的自旋关联研究中，他们利用中子散射验证了理论所预言的自旋关联长度各向异性。而在向列相的输运研究中，他们通过电阻测量发现了不符合简单伊辛模型描述的向列相临界涨落，并表明该涨落与电子向列型量子临界点直接相关。这些工作使我们更进一步理解了铁基超导体中向列相的相关问题。
　　首先介绍向列相自旋关联的研究。如图1所示，欠掺杂铁基超导体BaFe_2-xNi_xAs₂低温下的磁结构为铁位有效磁矩沿a方向反铁磁、b方向铁磁排列，两铁原子层之间也是反铁磁排列。因此，对于处于反铁磁有序态的单畴晶体，其低能自旋涨落仅在反铁磁波矢Q₁=(±1, 0)附近出现，而在其90°对称位置Q₂=(0, ±1) 为零。一旦升温进入高温顺磁态，自旋排列恢复各向同性，自旋涨落也同时在Q₁和Q₂两个点存在且强度相同。理论上预言，如果电子向列相由自旋自由度驱动的话，那么即使在高温四方相的顺磁态(晶格和磁性均满足四重对称)，也将出现二重对称的自旋涨落分布，即Q₁=(±1, 0)点自旋激发强度将大于Q₂=(0, ±1) 点，两者差异随温度降低而显著增大，同时，自旋关联长度也将出现类似行为，体系将形成所谓的“自旋向列相”。这种自旋激发强度的各向异性已经SC8组之前的中子散射实验研究被证实(Science 345, 657 (2014))。最近，他们进一步对自旋关联长度的各向异性进行了研究。图2给出了Q₁=(1, 0, 1)和Q₂=(0, 1, 1)在不同温度下的磁激发峰，可以看出随温度二者之间的变化是不同的。通过峰宽，可以获得自旋关联长度。他们发现，在结构相变温度之上，在峰强出现各向异性的同时（图3a），关联长度的各向异性也开始出现（图3b）。在峰强与关联长度各向异性之间存在着明显的关联，与自旋向列相理论预言符合的非常好（图3c）。另外，通过上述数据计算的动力学磁化率随温度的变化关系可以用朗道相变理论来描述(图3d)，说明其可以视为自旋向列相的序参量。该研究结果支持了自旋自由度作为电子向列相主要驱动力的图像，并于最近发表在Physical Review Letters 117, 227003 (2016)。
　　其次介绍电子向列相的量子涨落研究。由于电子向列相随掺杂逐渐消失，因此有报道认为可能存在电子向列相的临界点。但是在通过研究电阻随应变变化来获得向列相涨落时，并没有看到在最佳掺杂附近存在着最强的涨落信号。为了更好地研究电子向列相涨落，他们独立设计并搭建了一套基于压电陶瓷片的单轴压力装置(图4a)。压电陶瓷片既可提供拉伸力(张力)，又可提供压缩力(压力)，因此通过连续改变陶瓷片电压，可以让被测量的晶体感受从正到负的单轴压力(图4b)，准确地获得量子临界区信息。当应力沿着四方相的(110)方向时，由于铁砷面内二重对称的电阻特性，在结构相变温度之下可以获得类似磁滞回线的电阻随压力变化曲线(图4c)。当温度升高至结构相变温度之上时，电阻与压力成线性关系，其斜率随温度上升而迅速变小。这一结果与之前其他方法测量结果是一致的，即在(110)方向能够观测到向列相的信号。然而，令人惊讶地是，在沿着四方相的(100)方向施加应力，同样可以观测到电阻随压力线性变化（图4(d)），这与简单的伊辛向列图像是不符合的。之前的研究已经表明，(110)方向电阻随线性压力的依赖关系来源于向列相涨落。如果定义ζ为d(ΔR/R₀)/dp，其中ΔR、R₀和p分别为电阻变化、零压电阻及压强，在欠掺杂区域，ζ的温度依赖关系类似于居里外斯定律，通过拟合可以获得其平均场转变温度T’（图5(a)）。而在过掺杂区域，则在T_h处出现鼓包，表明该区域随温度降低而过度到量子无序区（图5(b)）。有意思的是，(100)方向的ζ也出现较强的掺杂依赖关系，且其在欠掺杂区域温度依赖关系无法用居里外斯定律拟合（图5(c)），而在过掺杂区域表现出和(110)方向类似的鼓包行为，二者之间成一定的倍数（图5(d)）。图6给出了BaFe_2-xNi_xAs₂体系的相图，其中T’和T_h相交在最佳掺杂处，表明存在着向列量子临界点。而(100)方向的ζ信号在该量子临界点处最强，强烈暗示该信号来源于费米面与向列相临界涨落的耦合，这样的量子临界点及其临界涨落行为不是简单的伊辛模型能够描述的。这一新的发现不仅拓宽了我们对铁基超导体向列量子临界涨落的理解，更对巡游电子体系中奇异量子临界点的理论研究提供了新的事例，这一工作发表在Physical Review Letters 117, 157002 (2016)。
　　上述研究工作由SC8研究组李世亮和罗会仟负责，其中向列相自旋关联研究主要由张汶良博士生完成，向列相量子涨落研究工作主要由刘曌玉博士生完成。除了本组其他老师和学生的贡献外，上述工作中的非弹性中子散射实验与德国慕尼黑的Heinz Maier-Leibnitz Zentrum (MLZ) 研究所的J. T. Park合作完成，在理论方面与中科院物理所的孟子杨和杨义峰等开展了密切合作，中科院物理所的任聪、单磊、邱祥冈和美国Rice大学的戴鹏程、中国原子能科学研究院的郝丽杰等在测量和数据讨论方面提供了很多帮助。
　　该系列研究工作得到了中科院B类先导、中科院青促会、科技部973项目、国家自然科学基金等项目的支持。

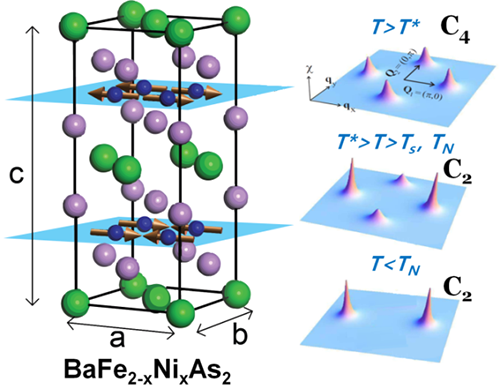图1. BaFe2-xNixAs2晶体结构、磁结构及自旋向列相

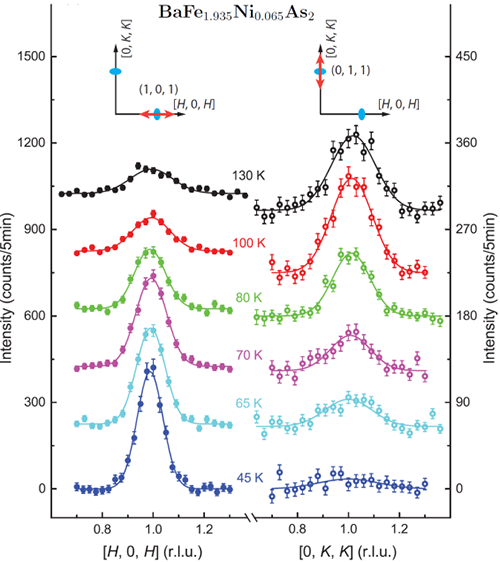图2. BaFe2-xNixAs2在Q=(1, 0, 1) 和 (0, 1, 1)处的磁激发分布。

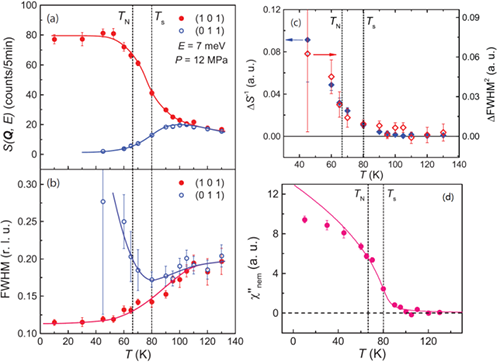图3. BaFe2-xNixAs2在Q=(1, 0, 1) 和 (0, 1, 1)处自旋激发强度和自旋关联长度的对比。

图4. 基于压电陶瓷技术的单轴压力下BaFe2-xNixAs2电阻测量。

图5. 单轴压力下BaFe2-xNixAs2电阻测量给出的向列相涨落序参量。

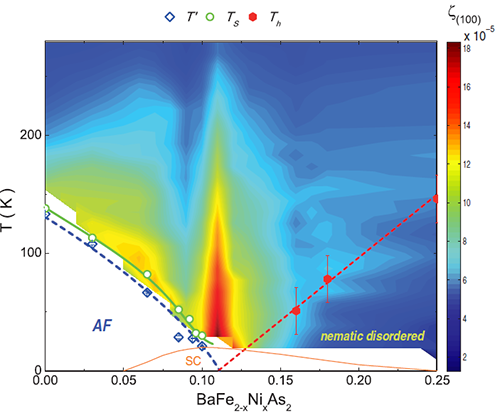图6. BaFe2-xNixAs2中电子向列相涨落的相图与量子临界点。