Kosterlitz-Thouless相变:拓扑元激发导致的特殊相变
戴希
今年的诺贝尔物理学奖授予了三位理论物理学家,分别是美国华盛顿大学的David J. Thouless, 普林斯顿大学的F. Duncan M. Haldane和布朗大学的J. Michael Kosterlitz, 以表彰他们在理论上提出了凝聚物质中的拓扑相变和拓扑相。作为在这一领域工作多年的研究者,衷心地为几位前辈的获奖而感到高兴,同时也深受鼓舞。

许多朋友来信,要求科普一下凝聚态物理学中的拓扑相,我在这里就向大家简单介绍一下。很多人都觉得拓扑这个数学概念很深奥,似乎很难跟生活中的物理现象发生联系,其实不然,生活中到处都有拓扑现象。比如说涡旋,就是一种常见的拓扑现象,我们每天清晨在洗漱台见到,在水流湍急的河边偶遇,在每一个台风过境的夜晚,我们怀着忐忑的心情等待。本次诺贝尔物理学奖得主Thouless先生和Kosterlitz先生发现的二维超流/超导体中的Kosterlitz-Thouless(KT)相变,就跟其中的涡旋激发有着密切的关系。因此作为本系列文章的开篇之作,先来讲讲涡旋激发和KT相变。
在介绍超流/超导体中的涡旋之前,我先向大家介绍一点非常基本的场论,考虑一个二维标量场,比如一个绷紧的鼓面,考虑它的横向振动,就是一个典型的二维标量场,它的运动可以由平面坐标(x,y)点处的振幅Z(x,y)来描写,它的集体运动模式就是我们熟悉的声波振动。与之类似,二维超流/超导薄膜的集体运动也可以由一个二维标量场来刻画,即平面坐标(x,y)点处的波函数相位θ(x,y),由于超流/超导相变破缺了U(1)对称性,当不存在集体激发时,刻画超流/超导体的波函数相位在空间各处是固定在一个值上的,可以假设为θ(x,y)=0。我们可以用图二中每一点的单位矢量与x轴的夹角来形象地演示相位场θ(x,y)。
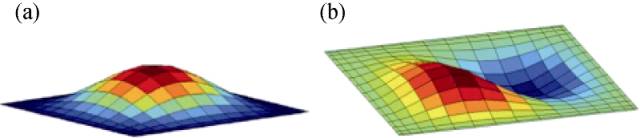
图一:鼓面的不同振动模式由一个标量场描述
接下来,我们来讨论系统的集体激发,它可以被分成两类模式,第一类是θ(x,y)在0附近做小幅振动,这种模式跟鼓面上的声波振动是非常类似的,如图二(b)所示。而另一种模式则是鼓面振动问题中没有的,也就是涡旋激发模式,为什么会存在这种不同呢?这是因为超导/超流问题和鼓面振动中的二维标量场是很不一样的,前者是紧致的而后者是非紧致的。紧致和非紧致是一个数学上的概念,大家别怕,它的意义很容易理解,通俗地说就是该标量的取值范围是在一个开放的空间(像鼓膜的横向振动),还是在一个收尾相连的封闭空间(如相位)。相位空间是一个典型的紧致空间,它是一个定义在0到2π之间的角度,而零度则严格等价于2π。正因为相位场的紧致性,导致了在超流/超导体系中另一类激发,拓扑型激发,也就是涡旋的出现。
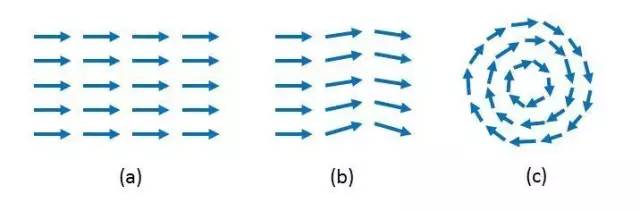
图二:超导/超流体波函数的相位构型
(a)基态构型(b)普通型激发(c)涡旋激发
一个典型涡旋的空间构型如图二(c)所示,围绕着涡旋中心,相位场θ(x,y)连续地从0变化到2π,注意由于0和2π的等价性,相位场的连续性并未被破坏。从图二(b)和(c)的对比中,可以看出涡旋和普通声波振动的不同,图二(b)中的声波激发构型可以通过对相位场施加连续形变来消除掉,而图二(c)中的涡旋在连续形变下只能移动位置而不能消除,把涡旋消掉的唯一办法就是通过连续形变,将一对手性相反(左旋和右旋)的涡旋挪到同一点上,让它们互相抵消。从拓扑学的角度看,具有单个涡旋激发的相位场构型跟没有涡旋的构型,是不能通过连续变形来互相转化的,属于不同的拓扑类,因此把涡旋激发称为是“拓扑型激发”。

图三:拓扑相变
1960年,Thouless和Kosterlitz两位先生通过漂亮的理论工作,推导出了在二维超流/超导体系中涡旋运动的理论模型,他们发现两种手性的涡旋(左旋和右旋)可以看成是被限制在二维平面内的正负“电荷”,互相之间存在二维“库仑作用”。更有意思的是,他们还发现随着温度的变化,这一体系中还存在着一种特殊的相变。在相变温度以上,存在着自由运动的涡旋,从而破坏了超导/超流的长程相位有序;而在相变温度之下,不同手性的涡旋只能两两配对形成束缚态,这时候存在着波函数相位的“准长程序”,也就是说相位关联随距离按幂函数而不是指数函数衰减。这种相位无序到“准长程序”的特殊相变,是涡旋游离态到束缚态转变所导致的,并不伴随着对称性的破缺,因此不能用朗道相变理论来刻画,后来以两位发现者的姓名命名为Kosterlitz-Thouless相变。在实验上,Kosterlitz-Thouless相变在许多超导薄膜中被观测到,这种由拓扑元激发导致的相变,受到了广泛的关注。此外,前苏联科学家Berezinskii也几乎完全独立地提出了这一相变机理,由于东西方冷战而被无情的铁幕隔在一边,不为许多人知晓,甚为遗憾,因此这一相变也被称为是Berezinskii-Kosterlitz-Thouless相变。
作者简介
戴希,男,1971年生。1993年毕业于浙江大学材料系,1999年在中国科学院理论物理研究所获得博士学位。1999年至2005年的6年间,先后在香港、美国等国的多个高等研究机构工作。长期从事强关联理论及计算方面的研究工作。2005年回国在中科院物理研究所工作,现任研究员、博士生导师。2010年入选中国科学十大进展;2011年"求是杰出科技成就集体奖";2011年获得“国家杰出青年科学基金”;2011年获第十二届“中国青年科技奖”;2011年“中国科学院杰出科技成就奖”。2012年全球华人物理学会“亚洲成就奖”(OCPA AAA [Robert T. Poe Prize])。
