“超固态(supersolid)”是指固体在维持周期性晶格的同时还存在超流现象。对于常规固体来说，这两种性质相互矛盾，但是在固体⁴He中却可能共存——这是由于氦原子作为最小的单原子分子具有极大的零点运动，相邻原子之间的波函数有非常大的交叠，从而形成宏观量子效应，从而可以承载超流。包括Andreev和Lifshitz[1], Leggett[2]在内的众多著名理论物理学家都预测在⁴He中存在“超固态”。虽然2004年在谐振扭摆实验中[3,4]得到的疑似“超固态”实验证据被证明是由弹性常数的反常畸变引起[5,6]，但是⁴He中是否存在“超固态”依然是一个未解之谜，并入选了Science杂志125周年遴选出的125个重大科学问题[7]。
　　最近，加拿大阿尔伯塔大学John Beamish研究组在极低温下利用压电陶瓷器件在固体⁴He一端施加挤压应力，并测量另一端压力变化[8,9]。研究人员发现测量端的压力缓慢线性上升，并最终达到饱和。压力上升意味着质量在应力作用下朝另一端流动。但与正常热激发产生的缺陷运动相反，该流动只在0.6 K以下产生，并且速率随着温度下降而增加，这是符合超流态的特征之一。进一步研究发现质量流动随着³He杂质浓度的增加而被逐渐抑制，这是符合超流态的特征之二。然而，这种质量流动是否具有相位相关性、无损耗性等其他超流典型特征还没有被验证，因此其超流特性还没有被最终确定。
　　³He作为比⁴He更轻的同位素，零点运动更加明显。但是由于是费米子，固体³He不可能出现“超固态”。因此可以通过研究固体³He中质量流动来判断⁴He中是否存在“超流态”。中国科学院物理研究所/北京凝聚态物理国家研究中心固态量子信息与计算实验室特聘研究员程智刚和加拿大阿尔伯塔大学John Beamish教授合作，利用压电陶瓷施加挤压应力的方法，测量³He中的质量流动行为[10]。实验表明固体³He中存在应力作用下的质量流动。但是与⁴He相反的是，质量流动在接近熔点（0.7 K）的高温区最为明显，随着温度下降流动速率单调降低，至30 mK时已经下降了2000多倍。研究还发现，在0.1 K以上流动速率对温度的关系符合热激发过程，而在0.1 K以下速率偏离了热激发行为而趋于饱和，表明质量的量子输运行为占据主导。在³He中质量流动速率与温度的关系不符合超流特征。这一发现支持在⁴He中存在“超固态”的观点。研究人员进而通过与微米级通道中固体³He流动速率对比，发现位错线运动是大尺度固体³He中的质量流动的主要原因。这一机制不仅适用于高温热激发区，也适用于低温量子输运区。
　　该成果首次对比了量子统计对量子固体中质量输运行为的影响，提供了支持波色量子固体中超固态存在的证据，并且揭示了费米量子固体中位错线运动行为，加深了人们对固体氦量子效应的理解。该成果发表在《物理评论快报》“Mass flow through solid ³He in the bcc phase”，Phys. Rev. Lett. 121, 225304 (2018)。该工作得到了科技部重点研发项目（2018YFA0305604）、基金委面上项目（11874403）、加拿大自然科学基金、松山湖材料实验室的资助。

图1. 在不同温度下挤压应力导致的压强变化。（a） T = 30 mK; (c) T = 100 mK; (d) T = 300 mK; (e) T = 700 mK.（a）中红实线表示施加挤压的时间；(b)和（f）分别为（a）和（e）中虚线框的放大图。（b）中红虚线拟合压强随时间线性上升的行为，得到上升速率为21 μbar/s。（f）中由于压强在2.5秒内已经饱和，因此估算上升速率为46.2 mbar/s。

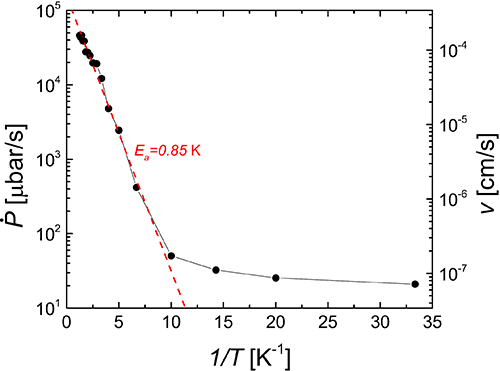图 2. 压强上升速率（即质量流动速率）随温度变化的Arrhenius图。在100 mK以上，流动速率满足热激发过程；在100 mK以下，流动速率趋于饱和，预示质量输运进入量子区域。

[1] A. F. Andreev and I. M. Lifshitz, Sov. Phys. JETP 29, 1107 (1969).
[2] A. J. Leggett, Phys. Rev. Lett. 25, 1543 (1970).
[3] E. Kim and M. H. W. Chan, Nature 427, 225 (2004).
[4] E. Kim and M. H. W. Chan, Science 305, 1941 (2004).
[5] J. Day and J. R. Beamish, Nature 450, 853 (2007).
[6] A. Haziot, X. Rojas, A. D. Fefferman, J. R. Beamish, and S. Balibar, Phys. Rev. Lett. 110, 035301 (2013).
[7] E. Hubble, Science 309, (2005).
[8] Z. G. Cheng, J. Beamish, A. D. Fefferman, F. Souris, S. Balibar, and V. Dauvois, Phys. Rev. Lett. 114, 165301 (2015).
[9] Z. G. Cheng and J. Beamish, Phys. Rev. Lett. 117, 025301 (2016).
[10] Z. G. Cheng and J. Beamish, Phys. Rev. Lett. 121, 225304 (2018).