量子纠缠是量子力学中一个基本概念，在经典世界没有对应，其基本表现是对贝尔不等式的违反，量子纠缠在量子计算和量子信息处理中起到核心的作用，各种纠缠态的制备是量子信息处理中一个重要课题，技术上也存在一定的挑战。但是另一方面，量子纠缠态在各种物理系统又是自然存在的，是系统量子特性的基本表现形式，特别在凝聚态量子多体系统，量子纠缠性质与新物态密切相关。
　　最近，中科院物理研究所/北京凝聚态物理国家研究中心固态量子信息与计算实验室Q03组范桁研究员、博士生曾昱，与北京计算科学中心博士后张煜然，浙江大学及北京计算科学中心游建强教授，日本理化所野理教授等合作，在利用多体量子纠缠性质刻画拓扑物态研究方面取得进展。
　　拓扑态的量子纠缠性质为凝聚态多体研究提供了新的视角和工具，拓扑物态的拓扑序可以用基于两体纠缠的拓扑纠缠熵或纠缠谱来描述和区分：它们体现为不同结构的长程纠缠，却不能简单地用朗道的局域序参量理论来描述。相比于两体纠缠，多体纠缠可以描述量子拓扑态更丰富复杂的纠缠结构性质，并提供更多的物理涵义，例如自旋压缩和量子费舍尔信息可以作为多体纠缠存在的充分判据条件。最近有研究组提出量子费舍尔信息可以作为多体纠缠的一个探测，并且可以描述低缠绕数的一维对称性保护量子拓扑态，但是这种方法并不适用于高缠绕数的拓扑序。团队尝试解决这些问题并且进一步地用多体纠缠来表征更特殊的拓扑序，通过考察扩展的 Kitaev 自由费米子一维链模型，这个模型具有 Z 对称性并且可以等价地用缠绕数和边界上局域的成对马约拉纳费米子数目来表征，对于高缠绕数的一维对称性保护的拓扑序，他们在缠绕数对应对偶空间中定义多体纠缠的度量，并且成功描述了具有不同缠绕数的一维对称性保护的量子拓扑态，同时，他们研究了二维的 Kitaev 蜂巢模型，通过引入特殊的对偶变换，这个模型的拓扑序可以用对偶空间的多体纠缠成功地描述。
　　通过引入对偶变换，用对偶空间的多体纠缠判据研究多体系统中不同的拓扑态，为凝聚态物理中的拓扑物态研究提供了新的工具和思路，同时受拓扑保护的多体纠缠可以作为重要的量子资源，应用于拓扑量子计算和量子精密测量中，文章发表在Phys. Rev. Lett. 120, 250501 (2018)。
　　以上工作得到国家自然科学基金委员会（11774406），科技部（2016YFA0302104, 2016YFA0300600）和中国科学院（XDPB08-3）的大力支持。
参考文献：
1.Yu-Ran Zhang, Yu Zeng, Heng Fan*, J. Q. You*, Franco Nori*,
Characterization of Topological States via Dual Multipartite Entanglement,
Phys. Rev. Lett. 120, 250501 (2018).

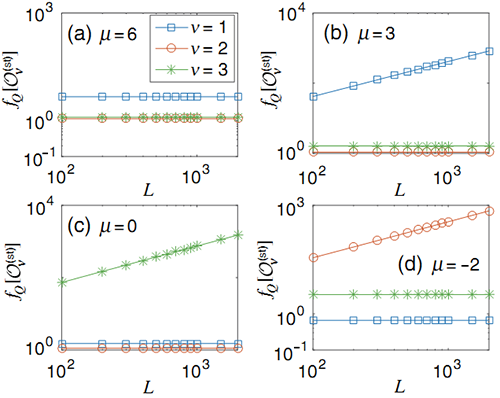图一：一维扩展Kitaev模型的基态纠缠性质可以用量子费舍尔信息刻画，可以发现量子费舍尔信息和不同拓扑相相关联。

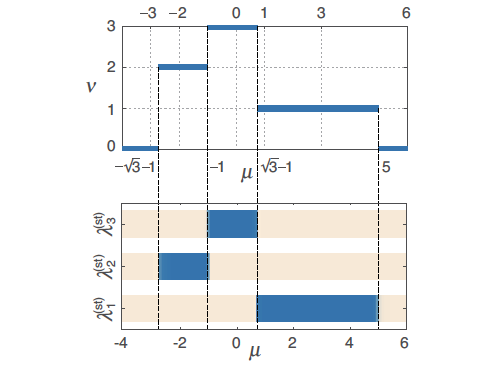图二：一维扩展Kitaev模型用缠绕数描述的相图与用量子费舍尔信息描述的相图完全对应， 表明量子多体纠缠与拓扑物态的关联。