作为典型的强关联电子系统,重费米子体系中的电子表现出丰富的多体量子行为,其准粒子的有效质量在低温下可以达到自由电子质量的上千倍,超过缪子的质量。这些低温重电子产生于晶格中每个格点上的局域f电子自旋与导带电子自旋的集体纠缠。随着温度降低或两种自旋之间相互作用的增强,临近格点间的自旋纠缠产生强烈的相干性,在量子力学效应的驱动下,局域的f电子被导带电子挟裹着运动,逐渐丧失了自己的局域性,最终与导带电子复合,产生了带有强烈f轨道特征的巡游重电子。这种巡游性和局域性的共存与竞争是产生非常规超导、非费米液体、量子相变等奇异量子效应的物理根源,而如何构建这一物理图像的理论描述,是重费米子研究的核心问题。
过去10年间,中国科学院物理研究所/北京凝聚态物理国家实验室(筹)的杨义峰研究员与合作者一起发展了重费米子的二流体理论,用局域自旋液体和巡游重电子两种流体近似描述f电子的这种局域和巡游的二重性。在此基础上总结实验规律,发现巡游重电子的贡献在很多物理测量如核磁共振、霍尔输运中表现出普适的温度演化规律,并建立了重费米子反常霍尔系数、核磁共振、重费米子超导、量子临界等奇异物性的唯象模型。有关二流体唯象理论的这些进展,在杨义峰最近应邀撰写的一篇综述文章中有简要概述[Rep. Prog. Phys. 79, 074501 (2016)]。
二流体唯象理论的成功迫切要求建立其具体的微观理论描述。最近两年,他们从不同的角度进行了尝试:
首先,如何表征f电子的局域/巡游性质?为此,杨义峰和博士生谢能(现已毕业)考虑到局域f自旋与导带电子之间的动力学纠缠,利用密度矩阵重整化群方法(DMRG)研究了一维Kondo-Heisenberg模型,发现在f电子从局域到巡游的转变过程中,其自旋关联谱函数在动量空间的分布特征发生了变化,这种变化或可来表征f电子局域或巡游的程度。这一研究提出了局域/巡游二重性的一种近似判依,但由于方法的限制,目前局限于零温一维系统,尚有待推广到有限温度和二维或三维体系。[Phys. Rev. B 91, 195116 (2015)]
其次,如何解释巡游重电子的普适温度依赖行为?为此,杨义峰和瑞士苏黎世理工学院的蒋密博士利用动力学团簇近似(DCA)对周期性Anderson模型的核磁共振Knight位移和磁化率进行了模型计算,发现两者之间对线性关系的偏离(即反常Knight位移)确实在一个很大的温度区间内具有二流体理论所预言的普适标度律。但是进一步计算却发现,其特征温度与计算所得的态密度和电阻的特征温度有很大差异,而实验(如在CeCoIn5中)观测则认为三者应有近似共同的特征温度。这一差异背后的物理根源尚有待进一步探索,可能意味着他们所采用的简单模型存在问题。[Phys. Rev. B 95, 235160 (2017)]
第三,能否建立起二流体行为的直观的平均场描述?为此,杨义峰和美国圣塔菲研究院的David Pines教授、英国剑桥大学的Gilbert Lonzarich教授合作,仔细分析了传统的基于Kondo-Heisenberg模型的平均场理论,发现一般的平均场处理忽略了f电子与导带电子杂化的空间涨落,导致了与实验的偏差。他们由此认为二流体现象可能超越了平均场理论的框架,需要考虑到集体杂化的空间和时间涨落的效应。前面基于DMRG和DCA方法的计算之所以能够取得部分成功,可能正与此有关。[Rep. Prog. Phys. 80, 024501 (2017)]
最近,他们在研究新的实验数据的基础上,发现在重费米子体系中存在两类普适标度律:一类是二流体理论预言的重电子随温度演化的普适对数依赖行为,这类标度律主要体现在核磁共振和霍尔系数等实验中;另一类是通常大家所熟悉的量子临界标度律,对温度呈现幂数的依赖性,主要体现在电阻和磁化率等测量中。通过对比分析发现,两类标度律出现的温度范围不同,第一类标度律伴随着重电子的产生,在相干温度下立即出现,在低温下会受到磁性量子临界涨落的影响,在磁性量子临界点附近会让位于第二类幂数标度律。这一结果表明两类标度律具有不同的物理起源,应该分别与重费米子体系中的两类量子临界点有关:第一类源自f电子的局域-巡游转变导致的杂化涨落,第二类源自局域f电子磁性量子相变导致的磁性量子临界涨落。[Proc. Natl. Acad. Sci. USA 114, 6250 (2017)]
基于以上考虑,他们提出了一个新的物理图像,认为应该从两类量子涨落耦合和竞争的角度理解重费米子体系的局域-巡游二重性及其诱导的各种奇异量子现象。发展这一图像,并构建其一般性的微观理论描述,是未来的主要研究任务。
以上工作得到了国家自然科学基金委(11522435、11174339)、科技部(2015CB921303)和中科院(XDB07020200、青促会)的资助。
[1] Y.-F. Yang, Rep. Prog. Phys. 79, 074501 (2016)
http://iopscience.iop.org/article/10.1088/0034-4885/79/7/074501
[2] N. Xie and Y.-F. Yang, Phys. Rev. B 91, 195116 (2015)
http://journals.aps.org/prb/abstract/10.1103/PhysRevB.91.195116
[3] M. Jiang and Y.-F. Yang, Phys. Rev. B 95, 235160 (2017)
https://journals.aps.org/prb/abstract/10.1103/PhysRevB.95.235160
[4] G. Lonzarich, D. Pines and Y.-F. Yang, Rep. Prog. Phys. 80, 024501 (2017)
http://iopscience.iop.org/article/10.1088/1361-6633/80/2/024501
[5] Y.-F. Yang, D. Pines and G. Lonzarich, Proc. Natl. Acad. Sci. USA 114, 6250 (2017)
http://www.pnas.org/content/114/24/6250
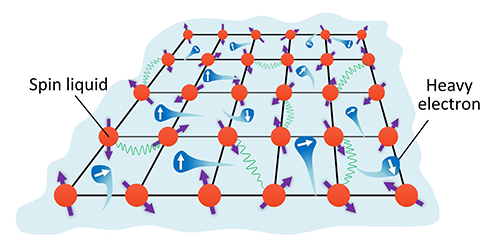 |
| 图1:重费米子晶格上由局域自旋液体和巡游重电子形成的二流体行为示意图 |
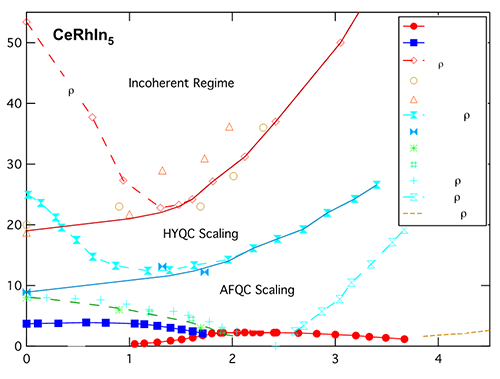 |
| 图2:重费米子材料CeRhIn5的压力-温度相图及其各种实验所给出的特征温度,其中HYQC代表杂化量子临界区,AFQC代表反铁磁量子临界区 |
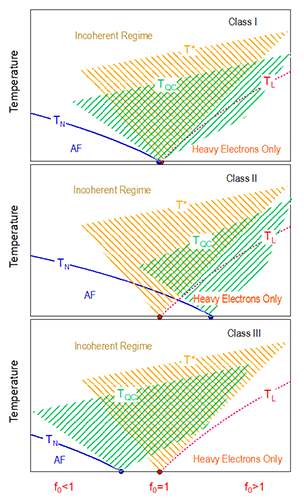 |
| 图3:三类重费米子材料、两类量子临界点及其相应的量子临界涨落示意图。其中f0表征杂化强度,T*为相干温度,TQC为磁性量子临界区的上边界,阴影示意两类不同的量子涨落,TL之下f电子完全巡游。 |
