(Ghost1984 /译)长久以来,麻省理工的工程师佩德罗·里斯(Pedro Reis)一直对物体如何褶皱有着浓厚的兴趣。比方说,与光滑球体相比,像高尔夫球那样遍布凹点的表面空气阻力更小。里斯想,如果一个飞行物体可以在指令下产生凹点或者褶皱,那么该物体便可在飞行过程中改变自身的空气动力特性。
里斯制作了一些硅胶试验球,抽出其中空气。他发现,压力下,有些球体产生了他想要的凹陷,而有些则呈现出迷宫般的扭曲褶皱图案。还有一些同时出现凹陷和迷宫纹。他的团队成员将这个有趣的现象告诉了麻省理工约恩·丹凯尔(Jörn Dunkel)领导的一个数学家团队,大家都对同一个问题深感兴趣:加热一层薄薄的油脂时,能够观察到类似条纹和漩涡状的图案,这种现象叫做Rayleigh–Bénard对流。这类现象有着经过简化、可以预测的方程式,那么, 凭什么褶皱现象不能也有一个简化方程呢?

当其中的空气被抽出,硅胶球就上出现了凹陷。图片来源:Denis Terwagne and Pedro Reis, MIT
早期的研究者采用逆向工作模式,从具体的褶皱效果出发,为单独褶皱案例进行推演,然而没有人能够在理论基础上简化出详尽的弹性方程,从而描述所有褶皱产生的行为——目前,尚未有普适的褶皱理论。在众多变量中,到底哪些重要,科学家们并不清楚。
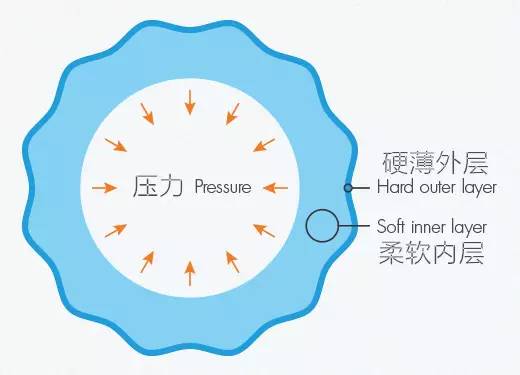
研究者的试验球由两部分组成:柔软的内层,硬而薄的外层。抽气导致内层向外层产生应力。是否产生褶皱,与外层厚度与整体曲率相关。图片来源 :Olena Shmahalo/Quanta杂志;资料来源:Pedro Reis
和数学家们一起,里斯重新审视他的团队所做的实验细节。当他们检查弹力球数据时,研究者们发现 ,控制图案形成的因素只有两个:底层曲率与其上褶皱层厚度之比,以及褶皱层受到的应力。在应力作用下,薄而平坦的表面会很快变成混合纹或者迷宫纹。顶部较厚、曲率更大的表面,将会形成六边形排列的凹点图案,但如果应力足够大(如里斯从小球内部抽气),最终也会变成迷宫纹。 释放应力后,表面复原。
“最有趣的地方在于,不是这两个参数重要,而是其他参数都不重要,”数学家之一、麻省理工的诺伯特·斯托普 (Norbert Stoop)表示,例如,研究者们发现,褶皱层的硬度对于结果毫无影响,“你可以将我们的理论应用于各种表面,月球、火星,或者葡萄。”

在压力作用下,曲面表面规则的凹点图案变成不规则的褶皱。图片来源: Norbert Stoop
“我告诉你,这是那种你会后悔自己没有抢先一步的事情,”阿默斯特麻省大学物理和材料学家克里斯蒂安·桑坦格罗(Christian Santangelo)评论道,“在一个领域略做研究,就能获得成果,我觉得,不是每个人都能遇到这种事。”
里斯的实验对象是乒乓球大小的宏观对象,肉眼可见。然而他的团队发现,微观球体也符合这一理论:其他实验室通过化学手段,增加氧化物薄涂层的应力,从而在微小的硅树脂聚合物半球表面也观察到了相似的图案。
当团队找到最终的简化方程时,他们发现最初的直觉是正确的。最终方程非常接近描述热油表面对流循环的流体力学方程。这个方程的广义形式可以用来描述,当一个变量改变时,有着常规排列的更大的系统突然变得不稳定,并最终被“破缺”打破其对称——例如,当具有常规晶体结构的冰融化成水时。普适的对称性破缺理论形成于七十年代,可是科学家们在非流体系统中,却没有发现类似的对应版本,斯托普解释道。
这项工作还帮助他人发现如何简洁描述其他的复杂弹性系统,桑坦格罗指出。在计算机的帮助下,研究者构建了一个复杂的模型,非常忠实地描述了手头的现象,但是对于认识背后的物理规律,模型并不能提供太多的帮助。“很多巨大的程序,基本上是将一切乱七八糟都扔进去,然后,当然就成了!”他说。“‘某些现象很简单,不需要太多描述’——这种想法很有用。“
新模型能够帮助研究者们理解自然界发现的很多重要褶皱系统,从星球表面的地势起伏,到小肠上的凹陷。即使被更为复杂的一些相互作用所掩盖,但任何扭曲和褶皱的东西,本质上都会具有这些基本形式。
对于合作者们来说,此次旅行远未结束。理论方程并不局限于球体,对于曲率不断变化、形状更为复杂的物体,褶皱如何产生,有太多需要研究的内容——这些试验,里斯的团队目前正在尝试。
“实验者和理论家的结晶是何等的美妙,”里斯如是说,“我们用自己搞不清楚的实验结果去为难他们,结果他们开辟了新的疆域。现在,轮到理论拿出新的问题挑战我们,而我们将用新的实验和模拟加以测试。”(编辑: 游识猷)
编译来源
Quanta magazine ,A Grand Theory of Wrinkles
