呼啦圈中的物理学
陈成钧
(美国哥伦比亚大学应用物理与应用数学系纽约10027)
美国麻省理工学院(MIT)网站上的电子刊《每周重大发明家》在2012年8月12日出版的一期中[1],记述了1958年Richard Knerr和Arthur Melin发明呼啦圈的一段历史。呼啦圈发明以后,很快就成为全世界青少年喜爱的体育用品。问世仅仅两个月,在美国就销售了2500万个。在1958和1959两年,在全世界就销售了一亿多个。呼啦圈运动不仅需要体力和耐久力,而且需要相当的技巧。美国健身运动促进会(American Councilon Exercise)在2011年发布了一份研究报告,以充分的科学数据说明,呼啦圈是最好的健身运动之一。加上美国第一夫人Michelle Obama和著名篮球运动员Shaquille O'Neal的公开演示和倡导,许多美国的体育馆已把呼啦圈运动设为正规的成人健身运动项目。技巧高的运动员还可以同时转动多个呼啦圈。在2008年,中国的金琳琳同时转动了246个呼啦圈,创造了金氏世界纪录。在2011年春节晚会上,她又以同时转动305个呼啦圈刷新了自己保持的世界纪录。图1显示了金琳琳同时转动5个呼啦圈的特技表演。这个特技表演是十分困难的。文章的最后一段将对此加以解释。
作为体育器材,呼啦圈的优点之一就是便于携带,随处都可以进行活动。旅行用的呼啦圈可以拆卸成八截,总重量约1公斤,因此可以放在手提行李中,见图2。

呼啦圈的物理学并不是平淡无奇的。几十年来,有不少研究论文发表。最重要的两篇,发表在读者众多的“American Journalof Physics”(《美国物理杂志》)上[2,3]。这两篇论文都把呼啦圈简化为在水平面内作近乎圆周运动的单个质点的受迫振动问题来处理,把人体的驱动简化为在的一条直线上的简谐运动或水平面内的椭圆运动(见图3)。研究重点是运用非齐次线性方程的解的稳定性的数学方法,找出呼啦圈稳定周期运行的条件。文献[2]假设支点A以圆频率ω在一段直线上作简谐运动,运动方程为
x=x0cosωt . (1)
呼啦圈则是一个质量为m的质点,它的唯一广义坐标是角度ϕ,拉格朗日方程是
ml2ϕ+βϕ+mω2lx0cosωtsinϕ=0,(2)
式中的l是从支点A到质点m之间的不变距离,β是阻尼系数。方程(2)的普遍解牵涉到相当复杂的数学问题,在文献[2,3]中有详细讨论。从解中可以得到呼啦圈稳定运转的条件。不论从运动员或教练的观点看,文献[2,3]中的单个质点平面运动的数学模型都过分简化了。真实的呼啦圈从来也没有在水平的二维平面中运动。由于重力,呼啦圈与水平面之间永远有一个不等于零的倾角。也是由于重力,呼啦圈会自动下滑。单纯的水平方向的力不可能使呼啦圈维持在水平面内运动。文献[4]和[5]报道了从生理物理学的角度对呼啦圈的工作原理所做的实验和理论研究。研究者们在人身体的各个部位和呼啦圈的多个点上设置了14个反光标志,用5台摄像机从各个角度记录运动过程,然后用数学统计方法对取得的数据进行分析。人体的运动是用一个具有18个自由度的机械系统来描述的。研究工作的主要结论有以下几点:
(1)呼啦圈可以被描写为一个刚体在三维空间中的运动。运动员的目标是保持呼啦圈的角动量的垂直分量稳定。
(2)运动员的动作是对呼啦圈实施周期性的冲量(力乘时间),来保持角动量恒定。
(3)克服重力是呼啦圈运动的第一要素。运动员必须对呼啦圈施加向上的冲量来平衡重力。
(4)水平方向的冲量必须与呼啦圈的运动保持准确的位相关系,来保持最大的能量传递。
(5)为达到上述目标,不同的运动员的肢体运动方式是不同的。
虽然文献[4]和[5]的实验和数值统计分析是扎实和细致的,但是缺乏简单明了的解析数学模型。本文将以文献[4]和[5]的概念为基础,建立一个解析的物理模型,最后获得一组可以用来指导实际训练的简单公式。这个物理模型的理论基础是几个基本力学原理,包括垂直方向的动量守恒,水平方向的离心力和身体作用力的平衡以及能量守恒。
图4是呼啦圈的三维刚体运动模型的示意图。首先考虑垂直方向的动量守恒。呼啦圈在稳定运转的时候,周期T和频率f的关系是
T=1/f. (3)
呼啦圈每旋转一圈,必须回到原位。在这期间,重力在垂直方向施加了一个向下的冲量,
ΔP=-MgT,(4)
式中,M是质量,g是重力加速度。为了回到原位,垂直方向的动量必须保持为零。为了克服重力,呼啦圈不仅需要接受水平力,而且需要接受垂直力。而垂直力只可以通过呼啦圈和人体之间的摩擦力来实现。通常的呼啦圈上缠着表面粗糙的布质胶带(见图2),并不只是一种装饰,而是增加摩擦系数的措施。专业的呼啦圈,则常常需要整个套上有一定粘性的软塑料管。为了实施垂直方向的力,运动员的膝关节不是挺直的,而是有一定的角度(见图4)。通过膝关节角度的变化,腰部可以通过呼啦圈和人体之间的摩擦对呼啦圈施加垂直向上的冲量。显而易见,在一个周期中,腰部对呼啦圈施加的平均的垂直向上的力是Mg(见图4)。

由于存在垂直方向的力和运动,呼啦圈不可能保持水平,而与水平面有一个倾角ϑ。这个倾角是由离心力和重力的比例决定的。把呼啦圈简化为一个在圆心作圆周运动的质点,从图4中可以得出回转半径ρ为
ρ=1/2(Dcosϑ-d), (5)
式中D是呼啦圈的直径,d是运动员腰部的直径。质点的线速度是v=2πfρ。离心力是
F=Mv2/ρ=4π2f2Mρ. (6)
从图4可以看出,倾角ϑ由离心力和重力的比例决定,即
tanϑ=Mg/F=g/(4π2ρf2). (7)
由此可以得出呼啦圈转动频率与倾角的依赖关系的公式:
f=1/2π√2g/(Dsinϑ-dtanϑ). (8)
通常,倾角ϑ都比较小。用弧度表示倾角,可以使用以下的近似公式:
sinϑ≅tanϑ≅ϑ. (9)
如用米表达长度,并注意到在数值上,π2≅g,就可得出呼啦圈转动频率f和倾角ϑ的近似公式为
f≅1/2π√2g/√(D-d)ϑ≅1/√2(D1-d)ϑ,ϑ≅1/2(D-d)f2.(10)
在呼啦圈实践中,另一个重要问题是腰部运动和呼啦圈转动之间的协调和同步。由于空气阻力和摩擦,呼啦圈的动能在不断地消耗。运动员必须通过腰部的水平运动,给呼啦圈补充动能。通常,运动员的腰部运动是直线运动,或者是前后摆动,或者是左右摆动。这种运动可以相当准确地描绘为简谐运动。问题是,腰部简谐运动和呼啦圈转动的相对相位必须精确地控制,才能有效地补充能量。在呼啦圈教练们的行话中,叫做寻找”着力点”(power point)。最佳同步运转的条件可以由能量转移的观点得出。
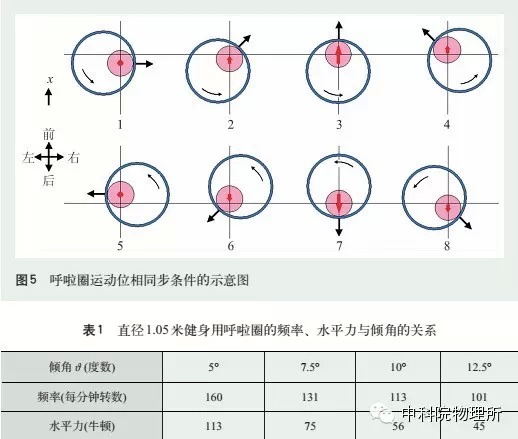
图5描述的是呼啦圈从右方向左方转动(或者说逆时针转动)的情况。这里,粉色圆面表示运动员腰部的截面,红色箭头表示腰部运动的速度。黑色箭头表示运动员腰部对呼啦圈施加的水平力,或者说呼啦圈受到的水平力。根据牛顿第三定律,运动员的腰部会感觉到一个强度相同而方向相反的反作用力。运动员的动作,就是根据这个反作用力来进行的。图5中位相1的位置是腰部开始向前移动的最佳时间。在位相2,3和4,呼啦圈受到的水平力是向前的,腰部的运动也是向前的,因此呼啦圈获得了正能量。在位相5,水平力指向左方,腰部运动速度是零。在位相6,7和8,呼啦圈受到的水平力是向后的,腰部的运动也是向后的,呼啦圈也会获得正能量。由于人体从接受到信息到开始行动需要大约0.1s的时间,用呼啦圈教练们的话来说,“着力点”(或者有意识地向前移动腰部的时间)是在呼啦圈将要达到腰部右方的一瞬间。同理,如果呼啦圈是在做顺时针转动,“着力点”是在呼啦圈将要达到腰部左方的一瞬间。
如果呼啦圈的旋转和运动员腰部运动之间相对于最佳情况有一个相位差,能量转移的效率就会大打折扣,甚至于完全不工作。假设运动员腰部沿x方向运动的速度是νx简谐的,即
vx=v0sin2πft,(11)
而呼啦圈受到的x方向的力也是简谐的,但是有一个位相差φ,
Fx=F0sin(2πft-φ).(12)
在每一个周期内,运动员给呼啦圈补充的能量E为
E=∫0T F0v0sin2πft sin(2πft-φ)dt=F0v0T/2cosφ.(13)
只有在位相为0时,能量才能够充分补充。位相差不等于0时,补充的能量就少了,甚至于成为负值。因此,呼啦圈不仅可以锻炼体力,而且可以锻炼神经反应的速度。大脑和小脑必须在大约0.1s的时间内根据腰部感觉到的力的变化给肌肉发出指令。

下面我们对驱动呼啦圈所需要的水平力做一个数量级的估计。体操用的呼啦圈的典型数据是:质量1.0kg,旋转频率每秒钟2圈,回转半径0.4m。根据(6)式,需要的水平力是66N(牛顿),大约7kg重。所以,连续运动十分钟以上,体力消耗也是很可观的。此外,为了保持身体上的水平力矩为零,脚和地面之间需要一个不断变化的水平力来达到平衡。这就解释了为什么常常看见健身者赤脚在有地毯的房间里玩呼啦圈(见图6)。表1是一个健身用呼啦圈的典型数据。直径是1.05m,质量是1.0kg,运动员腰部直径是0.25m。频率的单位是每分钟的转数,是由按秒计算的频率乘60得出的。
最后,我们对金琳琳的“五环”特技表演做一个分析。在表演的第一部分,她把5个呼啦圈分别放在身体的不同部位进行转动。从照片和录像可以看出,5个呼啦圈的位相是不同的。身体的5个不同部位必须独立地保持每一个呼啦圈的顺利运转。不但要使身体的5个不同的部位根据呼啦圈的旋转位相来施加水平力,而且还需要给每一个呼啦圈适当的提升力,来保持在预定的水平面内旋转。这是非常困难的。表演的第二部分就更难了。她把5个呼啦圈分别按顺序从身体的低处提升到高处,然后顺次从高举在头顶上的手上甩出去。在这个过程中,对每一个呼啦圈都需要在适当的时间施加适当的额外的提升力,才能使整个表演流畅自如。
参考文献
[1] http://web.mit.edu/invent/iow/hulahoop.html, "Fascinating factsabout the invention of the hula hoop by Knerr and Melinin 1958", MIT Inventorsof the Week, 8/12/2012 [2] Caughey T K. American Journal of Physics, 1960, 28: 104[3] Seyranian A P, Belyakov A O. American Journal of Physics, 2011, 79: 712 [4]Balasubramaniam R, Turvey M T. Biological Cybermetics, 2004, 90: 176 [5] CluffT, Robertson D G E, Balasubramaniam R. Human Movement Science,2008, 27: 622
(来源:《物理》2005年第一期)
