前两天小编的朋友圈简直被《开端》刷爆了，出于好奇小编花了一天时间补完了这部剧，从此再也不敢直视红色塑料袋。
《开端》主要讲述了主角李诗情和肖鹤云在一辆即将爆炸的公交车上不断经历循环，寻找真相，阻止爆炸的故事。
但是我发现，作者最后也没有解释为什么会出现 “循环”。于是，我陷入了沉思。
终于，在思考过人生的哲学后，我，岷 · G胖使徒 · 量子征服者 · 刷夜冠军 · 客发现这部剧的“循环“中竟然隐藏着这样深刻的物理原理！
蝴蝶扇动翅膀引起了龙卷风
《开端》的主角就拥有这样神奇的力量，于是他们想尽办法希望阻止炸弹爆炸。但是相比于计划中的响铃爆炸，意外撞到油罐车，手动引爆炸弹却是占了多数。
女主干扰司机行车，可能导致公交车撞向油罐车；直接报警，可能被警方认为是爆炸案凶手；武力制服陶映红，争夺高压锅可能会使炸弹提前引爆···
首先让我们看一个简单的数学递推关系
其中 r > 0 是一个预先设置的参数。例如，当 r = 2, x1=0.9 时，这个数列为
当 r = 2, x1=0.3 时，这个数列为
我们发现，这时无论初始的取什么值，数列最后都会收敛到0.5，然后让我们把参数调大，使 r = 2.5, 初始的 x 依然等于0.9. 此时计算数列得
可以看到，数列仍然会稳定到一个确定的数值，只不过这时需要计算更多次数。
但是，如果继续增大参数，当 r 增加到3以上，3.4以下后，最终的模式会是两个数字的交替出现，当 r 继续增加，序列会逐渐变成四个数字循环出现，然后是八个数字，十六个数字······
当参数继续增大到3.57后，这时的周期太长了，以至于无论一个人数多长时间都无法找出规律，或者说，周期性已经消失，进入了混沌。
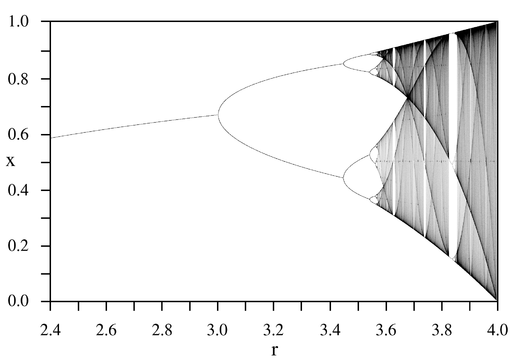
数列不动点（纵轴）与参数（横轴）之间的关系
让我们更进一步，看一个稍微复杂一点的例子。1963年，气象学家爱德华 · 洛伦兹提出了一个简化的大气对流模型，
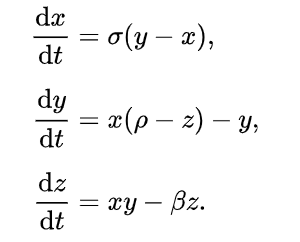
从此将人们对于混沌系统的研究推向了高潮。他在1963年解释道，“如果这个理论正确，一个海鸥扇动翅膀，将可能永远改变天气”。
在之后他使用了更加有诗意的解释，“一只南美亚马逊流域中的蝴蝶扇动了翅膀，将可能引起美国两周以后德克萨斯州的龙卷风”。因此，混沌又被形象地成为“蝴蝶效应”。
洛伦兹方程的一个解，描述了系统状态的演化 | 图片来源：Lorenz system - Wikipedia
可以看到，系统的状态仿佛一直在绕着两个圈转来转去。在上面的数列的例子中，当参数 r = 2 时，无论初始的值取多少，最后数列都会收敛到0.5。像这样的，一个系统有朝某个稳态发展的趋势，这个稳态就叫做吸引子。
吸引子是系统在演化过程中倾向的一组状态，适用于各种起始条件。吸引子可以是一个点，一个点集，也可以是一条曲线，甚至可以是具有分形结构的复杂集合。
同时，洛伦兹方程对初值条件是非常敏感的，因此在实际情况下，即使没有量子效应，我们对于未来的预测也可能会因为初值的微小差异而失败。
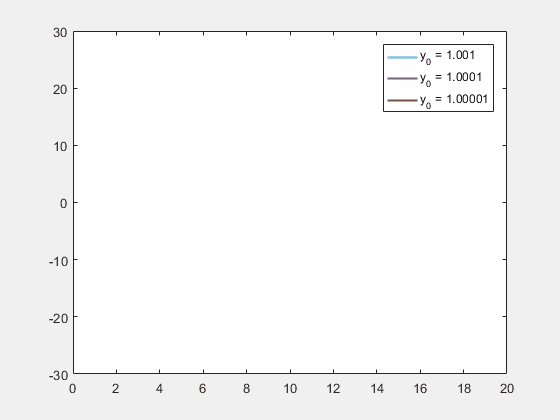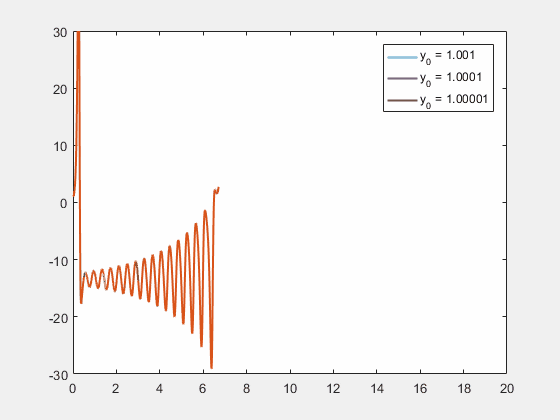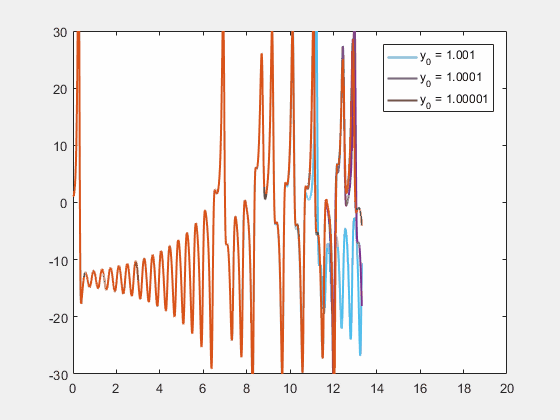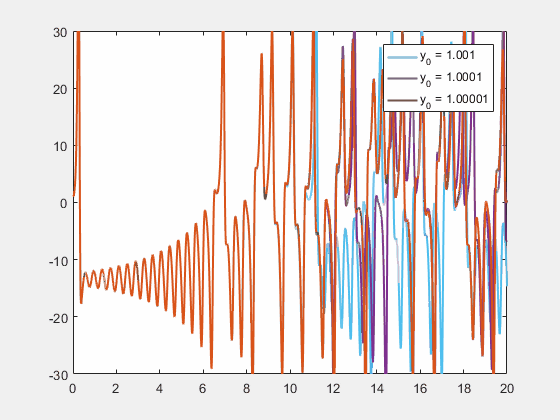
关于y变量的洛伦兹方程，x, z的初值条件不变。仅改变y的初值条件分别为1.001, 1.0001和1.00001。随时间的演化，差异越来越大 | 图片来源：Chaos theory - Wikipedia
非线性和混沌理论现在已经被广泛应用于各个领域，数学，物理，生物学，甚至在非自然科学领域的心理学，经济学都能看到他的影子。
例如，在经济学中，可以通过递归量化分析(Recurrence quantification analysis，RQA)的方法运用混沌理论。GIUSEPPE ORLANDO和GIOVANNA ZIMATORE利用从OECD数据库中检索到的美国GDP数据，对其做递归量化分析。他们检验了 RQA 在简单信号上的相关性，然后研究了在商业时间序列中的应用。
遍历所有可能
众所周知遇事不决量子力学，当我看到主角团可以一遍遍循环尝试各种办法阻止炸弹爆炸之后，我就知道，他们可能已经掌握了量子力学的奥秘了。
量子力学告诉我们，物质同时具有波的属性和粒子的属性，这就是“波粒二象性”。所以正如水波在经过障碍物时会激起花纹，光子、电子在经过狭缝时都会发生衍射。
双缝干涉结果图，最终会出现明显的衍射花样
为了解释这种现象，我们需要摒弃传统“路径”的思想，取而代之的是“概率”的思想。
在量子力学中，概率幅是描述系统行为的复数，这个复数的模方表示概率密度。在复平面上一个复数等价于一个矢量。
考虑一个电子衍射实验，从S点发射电子，在O点接收电子，中间经过一块屏障，屏上有两个狭缝A1, A2 。O点的电子的概率幅就是从A1, A2两条路径概率幅的叠加。
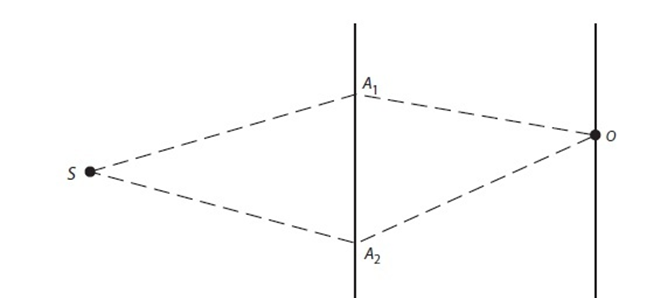
这时，有一个好奇的同学问，如果这是一块有三个狭缝（A1, A2 , A3）的屏障的话，O点的电子概率幅会是什么样的呢？很显然是A1, A2 , A3三条路径的叠加。
如果他接着问，如果再放一块带有狭缝的屏障的话，O点的电子几率幅会是什么样的呢？
这看起来是一个非常蠢的提问，不就是将所有的路径叠加吗？但是实际上却可以从这个概念出发，不断增加屏幕，不断增加狭缝，直至无穷多，这样就能够得到费曼路径积分了。
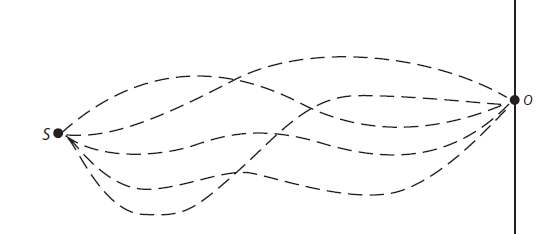
我知道大家不喜欢看公式（我也不喜欢），所以下面我们用一张图片来说明自由粒子的费曼路径积分的计算问题。
粒子从A点(start)传播到B点(end)有许多可能的路径，每一条可能的路径都会为B点的概率幅做出贡献，其贡献的权重表现为
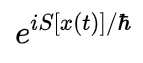
其中，S为作用量，ℏ为约化普朗克常数。
一组路径对自由粒子路径积分的贡献 | Path integral formulation - Wikipedia
我们需要将每一条路径得到的概率幅相加，反映在复平面上，就是将每一个小矢量箭头首尾相接，最后的总矢量就是从最开始的点到最后的点的连线。而概率幅的模方，就是B点粒子出现的概率。
请注意，上图的矢量AB表示的是粒子从A传播到B的概率幅，它的模方表示概率。下图用黑线框出来的区域表示路径积分后没有被抵消的一小块区域，当取ℏ趋于零的经典近似后，就会过渡到沿直线传播的经典情况。
在求和的过程中，那些很离谱的路径在求和过程中相互抵消，概率极小；只有在一小块区域内的路径不会抵消，当约化普朗克常数趋于零的时候，量子就会过渡到经典情况，这时就是我们熟知的“光沿直线传播”了。
回到开端
绕了这么一大圈，让我们来揭晓循环的秘密吧！
《开端》中男女主角一定熟知非线性物理，因为他们清楚的知道自己的动作会引发一连串反应，导致完全不同的结果；同时他们也有着扎实的量子力学基础，懂得路径积分就是将所有可能路径求和。因此他们一遍遍循环尝试，整理思路，最终阻止爆炸拯救所有人，就像是粒子最终找到了通往终点的 “道路” 一样。
所以说，这波是量子力学大胜利！