时间过得真快,一转眼已经是大年初六啦,大家是不是还在尽情享受假期呢?假期当然少不了游戏,在这最后的慵懒假日,不如让小编来带你玩个小游戏吧!在这个小游戏中,轻轻点击就可以围住可爱的猫猫,然后尽情…咳咳,享受冰冷的胜利吧!
回归正题。今天要讲的游戏叫做围小猫,2021年底在小编我的朋友圈里着实是火了一把,如果你还没有玩过,可以在搜索引擎中搜索“围小猫”。记忆力好的读者可能会记得,这款游戏并不是第一次火了,没错,它就是2014年曾在朋友圈大火过的“围住神经猫”的新皮肤!其原型可以追溯到更早。

游戏介绍
首先介绍一下游戏规则。起始小猫位于棋盘中心,6-8个障碍物会被预先随机放置在地图上。我方每次点击小圆点就可以在该处放置一个障碍物,而小猫也会向地图边缘移动一格,这样不断重复下去,直到猫猫被障碍物围住游戏胜利,或者到达地图边缘溜走游戏失败。
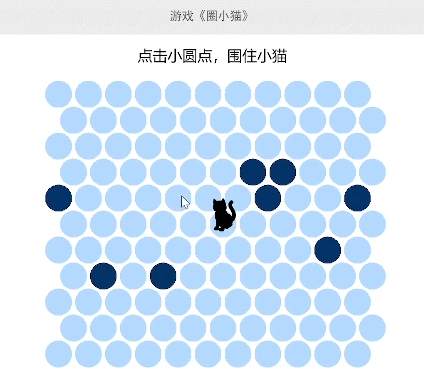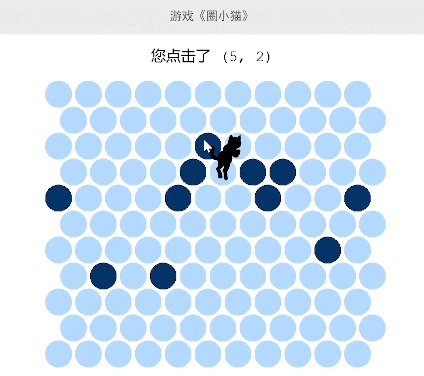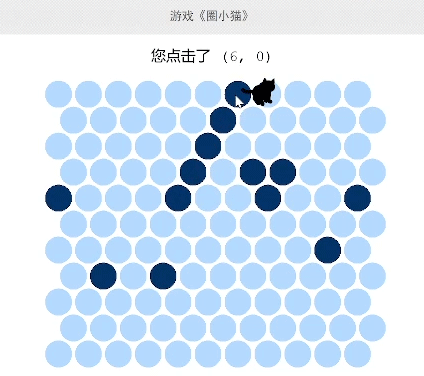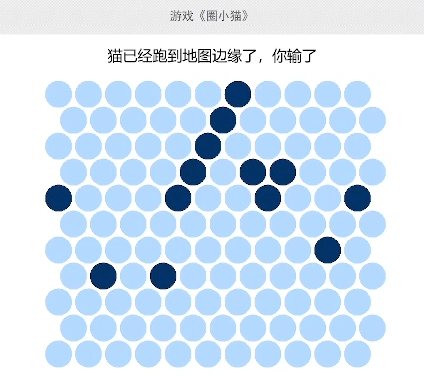
初上手的时候你会发现,这个游戏并不简单,几乎很难成功。因为棋盘其实并不大,猫只需要5步就可以跑出棋盘边界,很难将小猫堵住。
那么一个自然而然的问题是:如果棋盘足够大,可以保证将小猫堵住吗?在回答这个问题之前,请让我先介绍一下“天使问题”(angel problem)。
天使问题
天使问题首次见于1982年出版的《Winning Ways》一书,由书作者数学家约翰·H·康威(John H. Conway)提出。这是一个双方玩家分别扮演天使和恶魔的博弈游戏。游戏在一个无限大方格棋盘上进行,起始棋盘是空的。定义正整数k为天使的阶数,k阶天使每步可以跳到k*k范围内的任何一格,无论路上有没有障碍物。
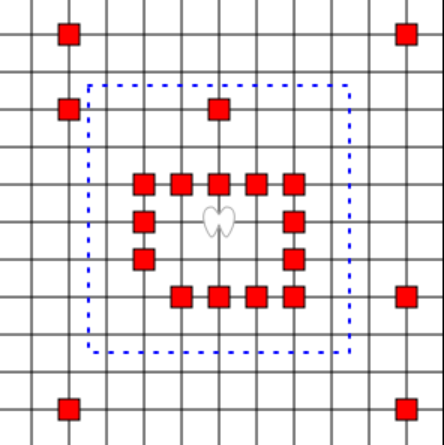
![]() 图1 蓝色虚线框内为3阶天使的移动范围|图源维基百科
图1 蓝色虚线框内为3阶天使的移动范围|图源维基百科
每一轮中,恶魔可以在棋盘上放置一个障碍物,但不可放在当前天使所在的位置,而天使可以移动到范围内未被放置障碍物的任何一处。若在一轮中,天使无法移动,则恶魔获胜。如果天使能无限地继续游戏,则天使获胜。康威已经证明(虽然他说是该书的共同作者伯利坎普展示给他的),只要棋盘大小大于32*33,k=1的情况下恶魔是必胜的。
![]()
为方便展示,这里将格点化为方格。如图2所示是一个33*33的棋盘,天使起始位于红色方格。无论天使开局怎么走,恶魔前8步只需将棋盘四周的8个黑格填上障碍物,这时天使必然位于中间的蓝色区域内,距离接触包围圈还有7步。
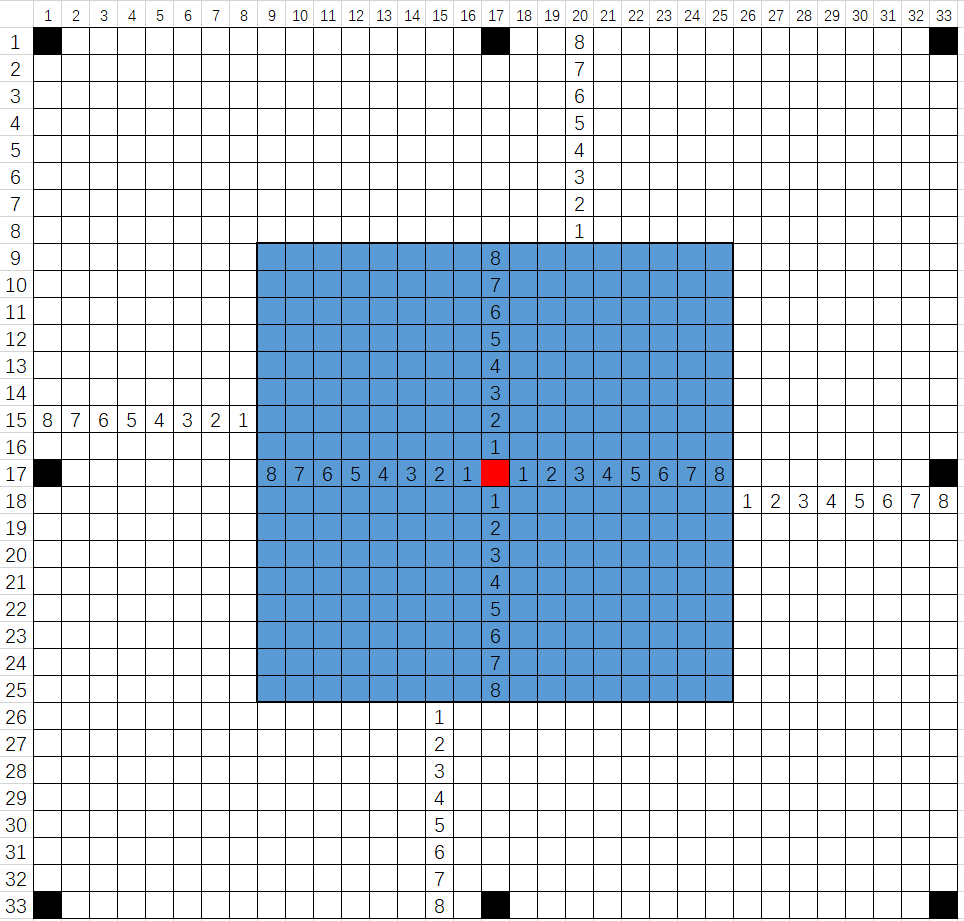
图2 1阶情形恶魔必胜|图源自制
而无论天使向哪个方向逃,恶魔都可以隔一格放一个障碍物这样逐渐缩小缺口,保证在天使接触棋盘边缘之前将缺口堵上,因此恶魔是必胜的。
一阶的天使问题告诉我们,只要棋盘足够大,让我们可以提前布置好包围圈,就一定能围住天使。而且天使问题中的棋盘是八连通的,即天使向横竖斜八个方向都可以移动,所以布置一个包围圈至少需要八步。而围小猫中的棋盘是六连通的,因此包围圈只需要6步。我们定义猫猫从空白棋盘中心逃脱的最少步数为棋盘的深度n,可以看到,围小猫游戏的棋盘深度为5。

图3 游戏棋盘的深度为5
丰富的游戏经验告诉我,n=5显然是不够的。如果要保证必胜,像天使问题里一样布置一个包围圈至少需要6个障碍物,也就是6步。因为猫n步就会逃出棋盘,而我们必须在猫逃脱之前花至少一步堵住逃脱的方向,所以棋盘的深度n至少应该为6+1+1=8。那么棋盘需要有多大才能保证必胜呢?答案就是n=8。图中偶数号格点为我方放的障碍物,奇数号格点依次为猫猫的行动轨迹,可以看到这种情况下,我方是必定获胜的。
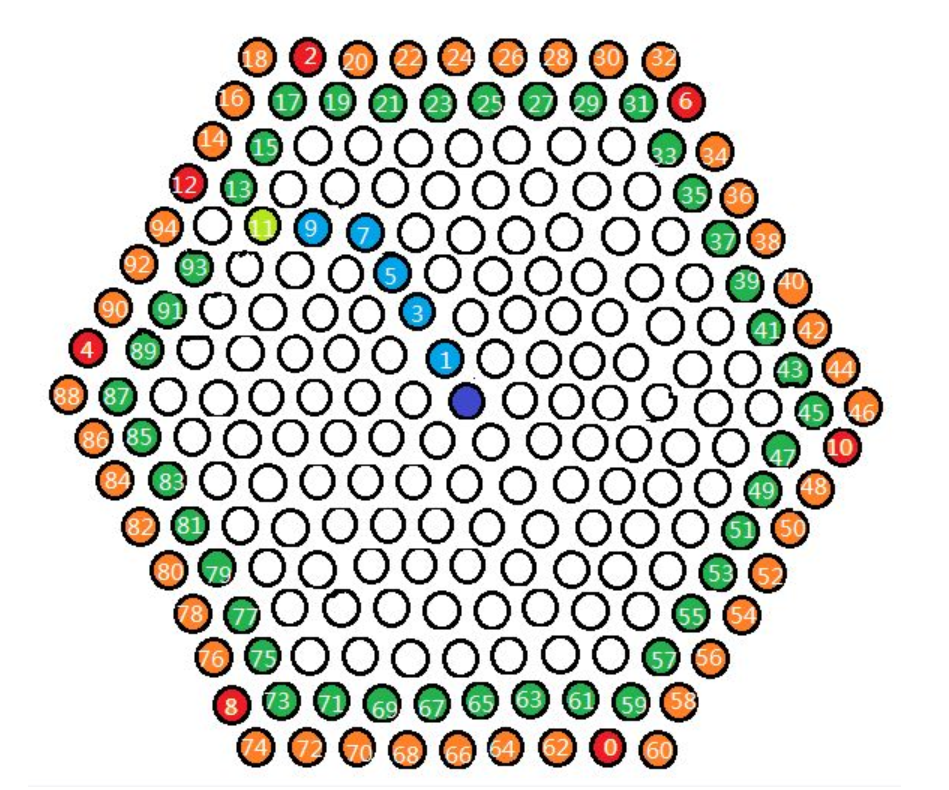
图4 n=8时的必胜策略|图源知乎
所以,只要棋盘的深度不小于8,即使是一个空白的棋盘,我们也是必定可以围住小猫的。相应地,在没有障碍物的情况下,棋盘深度小于8时我们是不可能围住小猫的。
那么,有障碍物呢?
终于回到了我们最初的问题:如何在一个n=5的棋盘上利用已有的障碍物围住猫猫。其实这里的思路还是一样的,那就是:先用若干步布置一个包围圈,然后通过围堵来完善包围圈。唯一的不同是,由于棋盘不够大,我们必须利用已有的障碍物来布置包围圈。和棋盘的深度一样,我们定义包围圈的深度为猫猫逃出包围圈的最少步数。很显然,包围圈越深,留给我们布置防线的步数就越多。
先来研究一下包围圈应该是什么样子的:包围圈应当是六边形,与棋盘形状相同,且每条边都经过每个经过格点的圆心,不允许斜着直接连。只有包围圈的每个顶点(如下面图6中的1-6号点)或者与该顶点相邻且在包围圈上的格点(如下图6中的7-15号点)有障碍物,才能起到挡住猫猫的效果。如果上述位置没有障碍物的话,就无法保证在猫猫被追赶到此处时闭合包围圈。

![]() 图5 红色连线没有经过所有经过格点的圆心,是错误的斜连。上面的深蓝色折线是正确的连法
图5 红色连线没有经过所有经过格点的圆心,是错误的斜连。上面的深蓝色折线是正确的连法
如果一个顶点或与其相邻且在包围圈上的格点上有障碍物,我们就称这个顶点已完成,定义一个包围圈的完成度为已完成的顶点数量。下面我们举一个例子来说明。


![]()
![]() 图6 一个包围圈的例子
图6 一个包围圈的例子
图6是一个包围圈的雏形,可以看到1,2,11,4,5号点都有障碍物,他们对应的顶点都已完成。但它并不是一个完整的包围圈,因为顶点6是未完成的。如果猫猫从右上往左上逃,我们堵住8号点后猫猫会逃至16号点,此时6,7两点均空,猫猫逃脱。顶点5虽然有障碍物,但它本身也是一个顶点,不能算作顶点6的相邻点。所以这个包围圈的完成度是5。
从棋盘深度为8的情形我们可以知道,在包围圈完成,即完成度为6时,如果猫猫距离包围圈至少有2格,我们根据猫猫的位置放障碍物来围堵就可以必胜。也就是说,必胜条件是包围圈深度+包围圈完成度至少为8。所幸,上图中的猫猫距离包围圈有3格,也就是说包围圈的深度是3,如下图所示,我们只需补上包围圈里缺失的点,就可以保证必胜。这就是看过本文的我们,第一步落在看似不需要优先围堵的6号点的原因。下面图7展示了图6例子中围猫的必胜方法。

图7 图6的必胜方法
需要注意的是,画包围圈也是有技巧的。比如下面这个图8就有AB两种画圈的方式,且包围圈的完成度均为5。如果按照红色的A方案规划4,5号点之间的包围圈,则包围圈的深度为2,5+2<8,无法围住猫猫。如果按照蓝色的方案B,则包围圈的深度为3,5+3=8,可以围住猫猫。所以画圈的方式也是很重要的哦!
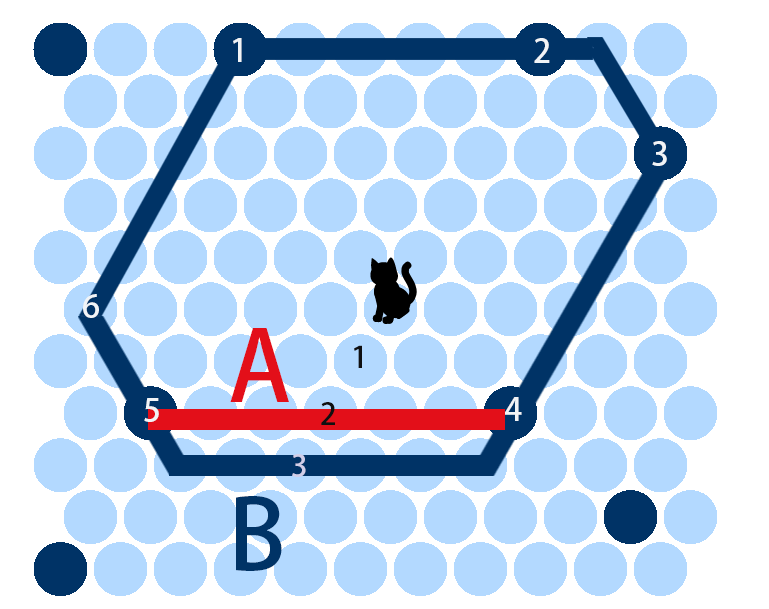
图8 两种不同的包围圈方式
然而,由于游戏条件的限制,初始只有6-8个障碍物,棋盘深度也只有5,所以大多数情况下都是无法必胜的,如果想围住小猫,就多多地刷新吧!
不过,实际上游戏里的这只小猫并不太聪明,它的逃脱逻辑只是一个单层的贪心算法:只考虑当前看来是最好的逃脱路线。所以我们可以利用这点设下陷阱,诱导猫猫走出多余的步数,从而赢下无法必胜的棋盘,有兴趣的读者朋友一定要去试一试哦。

围住猫猫的秘诀!
最后,让我们总结一下围住猫猫的秘诀吧!只需要简单的三步哦。
第一步:根据已有的初始障碍物划定包围圈,在保证有尽可能多顶点被完成的前提下,让包围圈的深度尽可能地大。第二步:判断包围圈完成度+包围圈的深度是否≥8?如果小于则无法保证围住猫猫,直接重置。第三步:先将包围圈完成,然后对应猫猫所在位置进行围堵即可获胜。
写在最后
还记得开头说的天使问题吗?这个问题其实并没有被完全解决。目前在天使的阶数k比较小,比如k=2的时候,数学家已经证明天使在无限大棋盘上是必胜的,但是对于任意有限阶的天使,哪方能必胜这个问题尚无答案。也许,能够解决这个问题的就是聪明的你。解决不了也没关系,至少,你学会如何抓住猫猫了,对吧?